Quarternion được sử dụng trong phép quay không gian. Trong phần 1 này, tôi sẽ nói về cách sử dụng sơ lược của nó trong phép quay không gian.
Bạn đang xem: Quaternion là gì
Các bài viết khác trong loạt bài về quaternion:
Quaternion được định nghĩa như là một số phức có ba thành phần ảo:

Đừng mường tượng quaternion là một cái gì đó bốn chiều, đầu bạn sẽ nổ tung. Các thành phần ảo

có thể được coi như ba vector đơn vị của trục tọa độ x, y, z. Và một quaternion có thể được viết lại như sau:

Với

là một vector trong không gian 3 chiều, và

là một đại lượng vô hướng chỉ độ lớn (nói chung là một con số). Dễ tưởng tượng hơn rồi đúng không!
Áp dụng vào phép quay không gian của chúng ta. Giả sử bạn có một vector trục quay

(vector

phải là vector đơn vị, tức
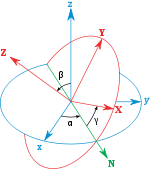
) và góc quay
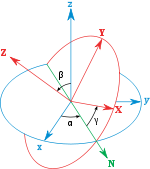
(dương khi quay cùng chiều với vector, theo nguyên tắc nắm tay phải) thì chúng ta sẽ có một quaternion quay như sau:
Ví dụ, bạn muốn tạo một phép quay một góc 120 độ (tức 2/3 pi radian) quay trục
. Đầu tiên chúng ta sẽ chuẩn hóa (normalize) vector

thành vector đơn vị
.

Và từ đó, chúng ta có quaternion cho phép quay là:
Để thực hiện phép quay, bạn cần một cái gì đó để quay. Ví dụ tôi có một điểm

trong không gian có tọa độ
được xác định trong không gian bởi vector
thì phép quay điểm

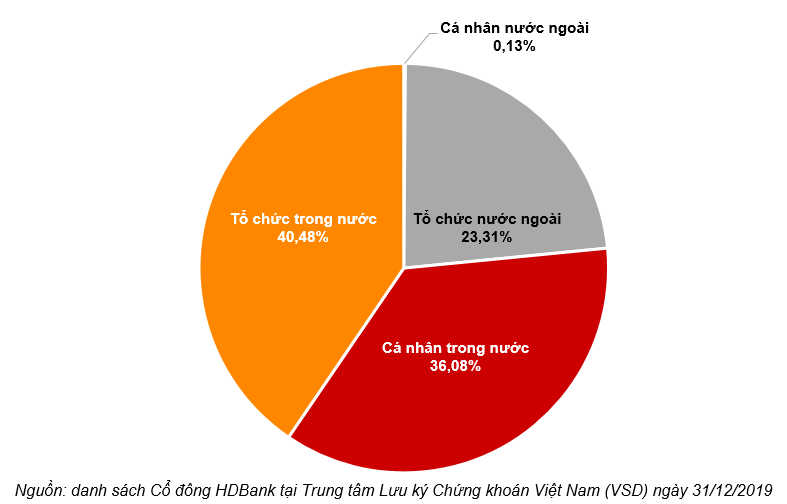
theo
được định nghĩa là:
Trong đó
là vector tọa độ của điểm

sau khi xoay. Và
là nghịch đảo của

. Cụ thể trong trường hợp này:

Trong trường hợp này, nghịch đảo bằng lượng liên hợp do trị tuyệt đối của quaternion trong phép quay bằng 1. Nếu bạn thắc mắc tại sao có công thức biến đổi quarternion, xin xem phần sau.
Xem thêm: Phim Chính Kịch Là Gì, định Nghĩa Về Phim Chính Kịch
Sau đó, chúng ta sẽ sử dụng phép nhân quartenion. Hãy ghi nhớ phép nhân quaternion không có tính giao hoán. Bạn có thể nghiên cứu thêm về phép nhân quaternion tại đây. Trong blog này tôi chỉ đề cập tới kết quả của phép nhân. Cho 2 quaternion

và
thì tích
là:
Sử dụng công thức trên để áp vào ví dụ của chúng ta (biến đổi

theo

) và làm phép nhân rất điên cuồng (tôi khuyên bạn nên dùng máy vi tính), chúng ta sẽ ra được:
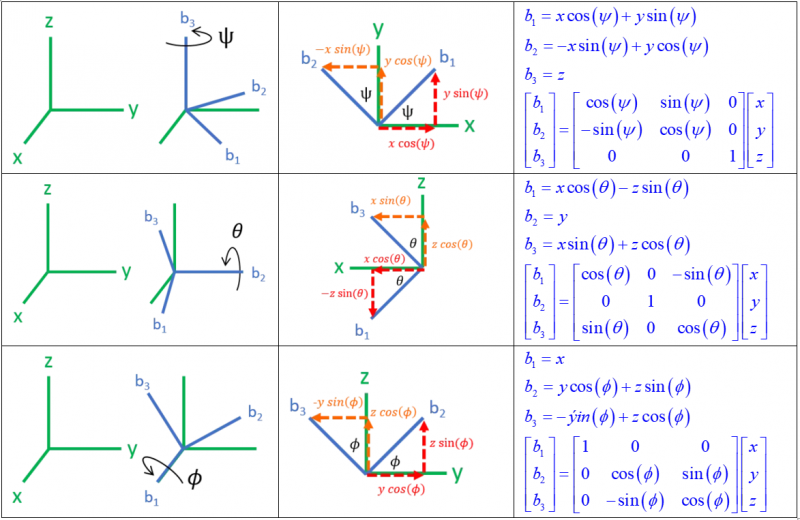
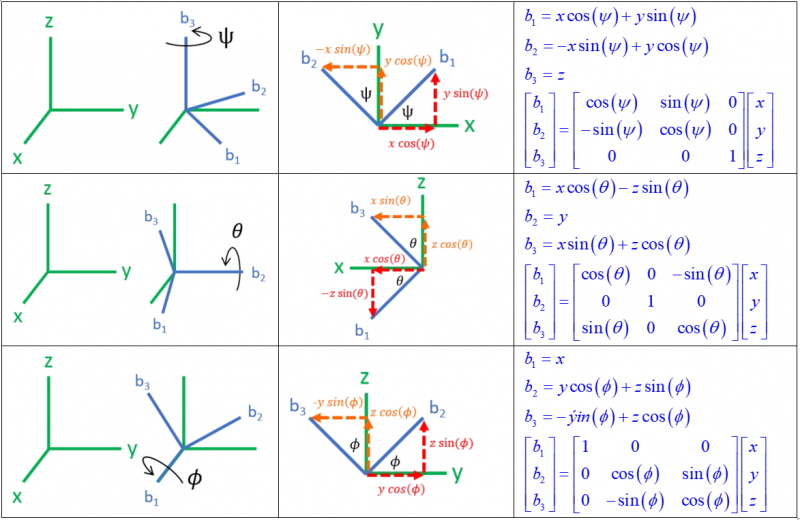
Hinh bên mô tả phép quay ví dụ của chúng ta. Chúng ta có thể thấy nếu chúng ta quay quanh trục

một góc 120 độ thì tọa độ

sẽ tráo cho nhau thành
. Phù hợp với kết quả của phép nhân ở trên.
Xem thêm: Cho Minh Hỏi Chữ Tiếng Anh Sở Giáo Dục Và đào Tạo Tiếng Anh Là Gì
Vừa rồi tôi vừa mới giới thiệu sơ lược về cách sử dụng quaternion trong phép quay. Trong phần sau, tôi sẽ nói đi sâu về phần toán, việc tối ưu hóa nó trong lập trình và so sánh với các phép biến đổi khác.
Chuyên mục: Hỏi Đáp