Bạn đang xem: Phân phối chuẩn là gì
Phân phối chuẩn là một trong các phân phối xác suất quan trọng nhất của toán thống kê, phản ánh giá trị và mức độ phân bố của các dữ liệu đang nghiên cứu. Thế giới tự nhiên, cũng như nhiều các quy luật kinh tế xã hội tuân theo luật phân phối chuẩn này, điển hình như: Chỉ số thông minh IQ, chiều cao, cân nặng, chiều dài giấc ngủ của con người, sự biến động giá trị cổ phiếu trên thị trường chứng khoán, hay mức thu nhập người lao động…
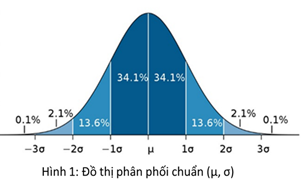
Phân phối chuẩn được đặc trưng bởi hai tham số là giá trị kỳ vọng µ (Muy) còn được hiểu là giá trị trung bình, và độ lệch tiêu chuẩn σ (Sigma). Trong khi giá trị µ là mức trung bình của tất cả các dữ liệu đang nghiên cứu thì σ phản ánh mức độ đồng đều của các dữ liệu này. Đồ thị của phân phối chuẩn có dạng hình chuông (Hình 1), nên đôi khi người ta còn gọi nó là phân phối hình chuông hay đường cong hình chuông – Bell Curve, và được biểu diễn bởi hàm mật độ xác suất:
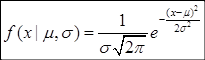
Xem thêm: Shoujo Là Gì – Shounen Là Gì Khác Nhau ở đâu
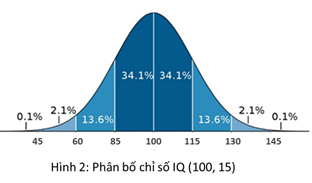
Chỉ số IQ – dùng để đánh giá mức độ thông minh của con người, tuân theo luật phân phối chuẩn (Hình 2). Phân phối này có giá trị kỳ vọng là µ=100, σ = 15, hay hiểu nôm na ra thì chỉ số IQ trung bình của dân số thế giới là 100, độ lệch tiêu chuẩn là 15.
Theo tính chất của phân phối chuẩn thì % diện tích các hình giới hạn bởi đường cong Bell Curve như sau:
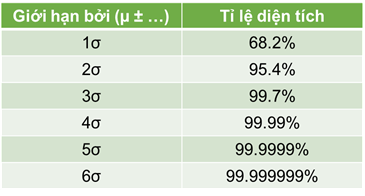
Như vậy, sẽ có 68.2% dân số thế giới có mức IQ từ 85 tới 115 (từ 100-15 tới 100+15) tức là trong khoảng (µ-σ, µ+σ). Khoảng này cũng được coi là khoảng mặt bằng chung của tập hợp, hay khoảng đa số. Nói cách khác, nếu gặp ngẫu nhiên 100 người trên hành tinh này, thường thì bạn sẽ gặp được khoảng 68 người có mức IQ “bình thường”. Vậy cơ hội để chúng ta gặp được “thiên tài” có mức IQ lớn hơn 160 như nhà bác học Albert Einstein hay Stephen Hawking là bao nhiêu? Rõ ràng với mức IQ 160 sẽ nằm ở µ + 4σ và cơ hội của chúng ta chỉ là (1-99.99%)/2 = 0.005%. Phân phối chuẩn nếu nhìn từ góc độ kiểm định giả thiết sẽ cho ta một mức sự tin cậy nhất định nào đó trước khi ta đi tới kết luận. Trong một mô hình nghiên cứu về một sự vật, hiện tượng nào đó bằng cách thu thập nhiều các số liệu về chúng, nếu xuất hiện một điểm số liệu cách mô hình được kiểm tra một vài độ lệch chuẩn, thì đây là bằng chứng mạnh mẽ cho thấy điểm số liệu đó không khớp với mô hình đó. Như vậy độ lệch chuẩn sigma σ được sử như một thước đo. Tuy nhiên, làm thế nào sử dụng thước đo này thì tùy thuộc vào tình huống cụ thể. Giáo sư John Tsitsiklis tại MIT, người giảng dạy Cơ sở Xác suất, phát biểu, “Thống kê là một nghệ thuật, với rất nhiều chỗ cho sự sáng tạo và sai lầm”. Một phần của nghệ thuật đó là xác định xem những số đo nào là có nghĩa trong một tình huống đã cho.
Xem thêm: Đất Cấp 1 2 3 4 Là Gì – Thành Phần Những Đất Đang Sử Dụng Hiện Nay
Ví dụ, trong xét nghiệm ADN để xác định huyết thống cha con, người ta thường lấy mức 4σ, tức trùng khớp 99,99% sẽ được kết luận là có huyết thống cha con. Nhưng mức này lại chưa đủ cho kết luận về những giả thiết đang thách thức kiến thức của các nhà khoa học về một hiện tượng quan trọng – Như việc phát hiện ra hạt hạ nguyên tử Higgs, người ta phải làm các thí nghiệm thực nghiệm có độ tin cậy 5σ tương ứng với sai số là ba phần mười triệu (độ tin cậy 99.9999%), đây cũng là mức mà các nhà vật lý hạt cơ bản sử dụng để công nhận một phát hiện mới. Ở góc độ ứng dụng giản đơn, chúng ta hoàn toàn có thể áp dụng mô hình phân phối chuẩn trong việc kiểm tra, đánh giá và phân loại học sinh trong trường học. Để phản ánh được trung thực trình độ nhận thức của học sinh, sinh viên, cũng như mức độ vừa sức của bài kiểm tra đánh giá kết quả học tập, kết quả thi kiểm tra nên có phân phối số điểm theo hình dạng đường cong chuẩn này. Theo đó, sẽ có khoảng 68,2% học sinh đạt mức điểm trung bình, mức 1σ. Mức 2σ, 3σ bên phải là các học sinh khá, giỏi chiếm tỉ lệ tương ứng là 13.6% và 2.1%, và tương tự đối với học sinh yếu, kém. Và như vậy, chúng ta trả lại ý nghĩa ban đầu cho các cụm từ “trung bình”, “khá”, “giỏi”. Một học sinh có học lực “trung bình” thực ra nằm ở khoảng mặt bằng chung của lớp (µ-σ, µ+σ), không cần phải quá tự ti về mức học lực này. Nhưng một học sinh có học lực “giỏi” trong khi tỉ lệ giỏi của lớp chiếm tới hơn 90%, thì cũng không mang nhiều ý nghĩa. Thực tế, chúng ta hoàn toàn có thể chọn các giá trị khác nhau của µ và σ tùy theo hoàn cảnh, ví dụ chọn mức trung bình µ=7 điểm, σ=1 điểm để khuyến khích động viên tinh thần học tập của học sinh, tuy nhiên chọn µ quá cao sẽ dẫn tới bệnh thành tích trong giáo dục, vốn là con dao hai lưỡi, đôi khi dẫn mang lại hiệu quả trái ngược. Toán học hiện đại không ngừng phát triển, nhưng các kiến thức về toán học dù cổ điển được tìm ra cách đây hàng thế kỷ nó cũng không bao giờ trở thành sai hay lỗi thời. Hiểu được bản chất vấn đề, nắm được quy luật tự nhiên, có một nền tảng kiến thức cơ bản tốt, sẽ là tiền đề để phát triển thành con người làm chủ tri thức, đóng góp tích cực cho sự phát triển chung của nhân loại.
Chuyên mục: Hỏi Đáp