Vật

Vật đại diện cho một đại lượng đo được và quan sát được hiện hữu ở 3 trạng thái Rắn, Lỏng Khí. Thí dụ như, Nước đá ở trạng thái rắn , Nước ở trạng thái lỏng , Hơi nước ở trạng thái khí . Mọi vật đều có một khối lượng vật chất bên trong một thể tích chứa vật chất . Tỉ lệ khối lượng vật chất trên thể tích vật chất cho biết Khối lượng riêng vật chất . Mọi vật tạo từ các phần tử vật chất nhỏ nhất được gọi là Nguyên tử . Nguyên tử được tạo ra từ các phần tử nhỏ hơn là proton, notron và electron .Theo lý thuyết Bohn về cấu tạo của nguyên tử, nguyên tử có cấu trúc gồm các “đám mây” electron mang điện tích âm xung quanh hạt nhân nguyên tử mang điện tích dương. Có 3 loại điện tử Điện tử âm, Điện tử dương, Điện tử trung hòa

Trạng thái vật chấtRắn . Đồng (Cu) , Sắt(Fe) , …Lỏng . Nước(H2O), …Khí . Ôxygen (O2)
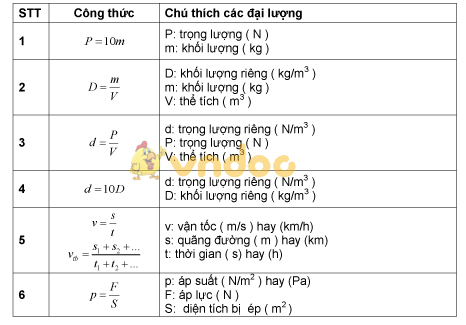
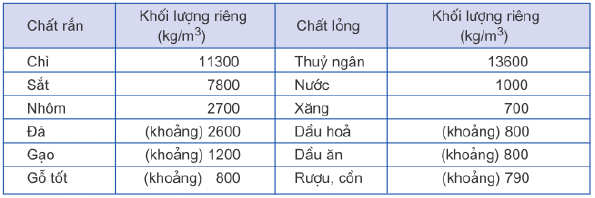
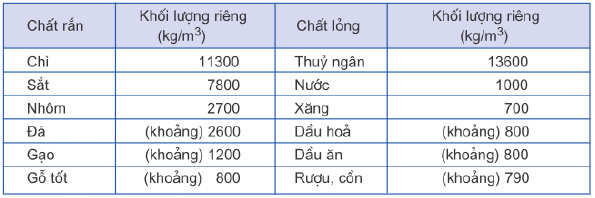
Dung lượng vật chất D = M V {displaystyle D={frac {M}{V}}}

*

Mô hình nguyên tử Rutherford

*

Các lực cơ bản

Lực di chuyểnLực làm cho vật di chuyển F a {displaystyle F_{a}}

*

a = v t {displaystyle a={frac {v}{t}}}

*

a = v t {displaystyle a={frac {v}{t}}}

*

a = v − v o t − t o {displaystyle a={frac {v-v_{o}}{t-t_{o}}}}

*

a = d v ( t ) d t {displaystyle a={frac {dv(t)}{dt}}}

*

a = ω r t {displaystyle a={frac {omega r}{t}}}

*

v = d d t s = d d t r θ = r d d t θ = r ω {displaystyle v={frac {d}{dt}}s={frac {d}{dt}}r heta =r{frac {d}{dt}} heta =romega }

*

y ( t ) = A sin ⁡ ω t {displaystyle y(t)=Asin omega t}

*

i = A sin ⁡ ω t {displaystyle i=Asin omega t}

*

V C = − V L {displaystyle V_{C}=-V_{L}}

*

B ″ ( t ) = − ω B ( t ) {displaystyle B^{“”}(t)=-omega B(t)}

*

B ″ ( t ) = − ω o B ( t ) {displaystyle B^{“”}(t)=-omega _{o}B(t)}

*

m a = − k y {displaystyle ma=-ky}

*

y = A sin ⁡ ω t {displaystyle y=Asin omega t} d 2 i d t + 1 T = 0 {displaystyle {frac {d^{2}i}{dt}}+{frac {1}{T}}=0}

 Z L = − Z C {displaystyle Z_{L}=-Z_{C}} L d i d t + 1 C ∫ i d t + i R = 0 {displaystyle L{frac {di}{dt}}+{frac {1}{C}}int idt+iR=0}

*

∇ × E = − 1 T E {displaystyle
abla imes E=-{frac {1}{T}}E}

*

m {displaystyle m}

*
Phản ứng điện DC V = I R {displaystyle V=IR}

*

I = Q t {displaystyle I={frac {Q}{t}}}

*

I = B L {displaystyle I={frac {B}{L}}}

*

L d i d t + i R = 0 {displaystyle L{frac {di}{dt}}+iR=0}

*

C d v d t + v R = 0 {displaystyle C{frac {dv}{dt}}+{frac {v}{R}}=0} d 2 i d t + 1 L C = 0 {displaystyle {frac {d^{2}i}{dt}}+{frac {1}{LC}}=0}

Z C = − Z L {displaystyle Z_{C}=-Z_{L}}

L d i d t + 1 C ∫ i d t + i R = 0 {displaystyle L{frac {di}{dt}}+{frac {1}{C}}int idt+iR=0}

*

T = R C {displaystyle T=RC}

*

T = L R {displaystyle T={frac {L}{R}}} T = R C {displaystyle T=RC} T = L R {displaystyle T={frac {L}{R}}}

*
 v o v i = ( 1 1 + j ω T L ) ( j ω T H 1 + j ω H ) {displaystyle {frac {v_{o}}{v_{i}}}=({frac {1}{1+jomega T_{L}}})({frac {jomega T_{H}}{1+jomega _{H}}})}

*
 v o v i = ( 1 1 + j ω T L ) ( j ω T H 1 + j ω H ) {displaystyle {frac {v_{o}}{v_{i}}}=({frac {1}{1+jomega T_{L}}})({frac {jomega T_{H}}{1+jomega _{H}}})}

*

ω = ω 1 − ω 2 {displaystyle omega =omega _{1}-omega _{2}}

*
Bộ biến đổi chiều điện
*
Bộ biến điệnLối mắc Tính chất
Bộ biến điện
*

Tăng điện . v s = v p N s N p {displaystyle v_{s}=v_{p}{frac {N_{s}}{N_{p}}}}

Bình ắc quy
Điện cựcPin cục
Quang tuyến nhiệt điệnPin mặt trời
Biến điện AC ra điện DCBiến điện + 4 cầu điot + Tụ điện cực + Điot ổn điệnĐiện cực tạo ra Điện DC v ( t ) = V sin ⁡ ω t {displaystyle v(t)=Vsin omega t}

*

Điện từ

Oerst khám phá ra rằng la bàn đi lệch khi nằm kề cộng dây điện dẩn điện . Khám phá này đặt nền tảng cho điện từ . Ampere khẳng định cộng dây dẩn điện tạo ra từ trường giống như từ trường của nam châm có khả năng hút từ vật nằm kề nam châm . Điện từ một hiện tượng tìm thấy trong tương tác giửa dẩn điện và điện có dòng điện khác không tạo ra từ có từ trường giống như Từ trường của Nam châm .

Bạn đang xem: P là gì trong vật lý

Xem thêm: – ‎minion Rush Trên App Store

Xem thêm: Win 10 Enterprise Là Gì

Một vật có khả năng hút kim loại nằm trong từ trường

| | = (-)

Điện tích âm = (+)Điện tích dương
*

Ampere khám phá cho thấy khi có một lực làm cho điện tích đứng yên di chuyển thẳng hàng tạo ra một điện trường . Lực này được gọi là Lực động điện hay còn được gọi là Lực Ampere tính bằng công thức

F E = Q E {displaystyle F_{E}=QE}

tạo từ các đường lực điện hướng ra bao quanh lấy điện tích
Điện trường của dipole
*
Điện trường của tụ điện
*

Từ trường

Từ trường . Môi trường tạo ra từ các đường lực từ bao quanh lấy vật dẩn từ

Từ trường của điện tích âmĐiện tích âm có vòng tròn từ của các đường lực từ hướng lên
Từ trường của cộng dây thẳng dẩn điệnTừ trường là một tập hợp của các vòng tròn lực từ bao quanh các điện tích điểm
Từ trường của cuộn tròn dẩn điện
*
 V = I R {displaystyle V=IR}

*

V = d B d t = L d i d t {displaystyle V={frac {dB}{dt}}=L{frac {di}{dt}}}

*

Từ dung L = N μ l {displaystyle L=N{frac {mu }{l}}}

*

∇ 2 B = − ω B {displaystyle
abla ^{2}B=-omega B}

*

∇ × E = − ∇ B {displaystyle
abla imes E=-
abla B}

*
 B = L i = N μ o l i {displaystyle B=Li={frac {Nmu _{o}}{l}}i}

*
 f = f o {displaystyle f=f_{o}}

*
Định luật phóng xạ vật đen
Định luật Công thức
Định luật Planck B ν ( T ) = 2 h ν 3 c 2 1 e h ν k T − 1 , {displaystyle B_{
u }(T)={frac {2h
u ^{3}}{c^{2}}}{frac {1}{e^{frac {h
u }{kT}}-1}},}

*

Quang tuyến nhiệt của phóng xạ alpha đi lệch hướng xuống Quang tuyến nhiệt của phóng xạ beta đi thẳng không lệch hướngQuang tuyến nhiệt của phóng xạ gamma đi lệch hướng lên

Phóng xạ nguyên tử

Trạng thái điện tửHình Công thức toán
Điện tử động
*

v = 2 m ( h f − h f o ) = 2 m ( n h f o ) {displaystyle v={sqrt {{frac {2}{m}}(hf-hf_{o})}}={sqrt {{frac {2}{m}}(nhf_{o})}}}

*

r = 1 2 π n h f m v {displaystyle r={frac {1}{2pi }}{frac {nhf}{mv}}}

*

v = 1 2 π n h f m r {displaystyle v={frac {1}{2pi }}{frac {nhf}{mr}}}

*

n = 2 π r m v h f {displaystyle n=2pi r{frac {mv}{hf}}}

*

Lượng tử

Lượng tử đại diện cho một vật lượng không có khối lượng di chuyển dưới dạng Phóng xạ sóng điện từ ở vận tốc cực nhanh bằng với vận tốc ánh sáng thấy được mang theo Năng lượng lượng tử của một năng lượng nhiệt được gọi là Quang tuyến nhiệt điện từ hay Photon . Lượng tử được tìm thấy từ Phóng xạ vật . Lượng tử có ký hiệu h là một hằng số có giá trị không đổi được gọi là Hằng số Plank của công thức

h = p λ {displaystyle h=plambda }

Tính chất lượng tử

Công thức lượng tử h = p λ {displaystyle h=plambda }
Giá trị lượng tửLượng tử là một hằng số không đổi có giá trị bằng hằng số Planck

h = × 10 − 34 {displaystyle h= imes 10^{-34}}

*
Lưởng tính sóng hạtTính sóng , λ = h p {displaystyle lambda ={frac {h}{p}}} Tính hạt , p = h λ {displaystyle p={frac {h}{lambda }}}

*
Động lượng lượng tử p = h λ = h k 2 π = ℏ k {displaystyle p={frac {h}{lambda }}=h{frac {k}{2pi }}=hbar k}

*

p = E C = h f C = h λ {displaystyle p={frac {E}{C}}={frac {hf}{C}}={frac {h}{lambda }}}

*
Bước sóng lượng tử λ = h p = ω f = C λ {displaystyle lambda ={frac {h}{p}}={frac {omega }{f}}={frac {C}{lambda }}}

*
Năng lượng lượng tử hay Quang tuyến lượng tử Tiếng anh là Photon E = p C = h f = h ω 2 π = ℏ ω {displaystyle E=pC=hf=h{frac {omega }{2pi }}=hbar omega }

*
Trạng thái quang tuyến lượng tửQuang tuyến nhiệt quang

v = ω o = 1 μ o ϵ o = C = λ o f o {displaystyle v=omega _{o}={sqrt {frac {1}{mu _{o}epsilon _{o}}}}=C=lambda _{o}f_{o}}

*

E = h f o {displaystyle E=hf_{o}}

*

h = p λ o {displaystyle h=plambda _{o}}

*

Quang tuyến nhiệt điện v = ω = 1 μ ϵ = C = λ f {displaystyle v=omega ={sqrt {frac {1}{mu epsilon }}}=C=lambda f}

*

E = h f {displaystyle E=hf} h = p λ {displaystyle h=plambda }

Theo Heinsberg , quang tuyến lượng tử chỉ có thể tìm thấy ở một thời điểm thời gian của cùng một giá trị lượng tử

Δ λ Δ p = 1 2 h 2 π = h 4 π = ℏ 2 {displaystyle Delta lambda Delta p={frac {1}{2}}{frac {h}{2pi }}={frac {h}{4pi }}={frac {hbar }{2}}}

Tính chất xác định trạng thái Heiseinberg

Theo Heinsberg , trạng thái của quang tuyến chỉ có thể tìm thấy ở một thời điểm thời gian của cùng một giá trị lượng tử Δ λ Δ p = 1 2 h 2 π = h 4 π = ℏ 2 {displaystyle Delta lambda Delta p={frac {1}{2}}{frac {h}{2pi }}={frac {h}{4pi }}={frac {hbar }{2}}}

Sóng lượng tử

Sóng lượng tử là một loại sóng vật chất của một lượng tử có lưởng tính sóng hạt mang theo năng lượng lượng tử . Sóng vật chất, có thể biểu diển bằng hàm số sóng, có thể là hàm của vị trí và thời gian. Tuy nhiên, nó cũng có thể được biểu diễn như là hàm số phụ thuộc vào các biến số khác Với hạt vật chất tổng quát, các thí nghiệm giao thoa có sử dụng các máy đếm hạt cho thấy: Xác suất trong mỗi đơn vị thời gian, để tìm thấy một hạt, trong một vùng thể tích nhỏ quanh một điểm, tỷ lệ với bình phương độ lớn của sóng vật chất tại điểm đó . Với một hạt chuyển động tự do trong chân không, hàm sóng của nó, giống như với photon đã nêu ở trên, là:

Ψ ( r , t ) = e i ℏ p . r e − i ℏ E t {displaystyle Psi (mathbf {r} ,t)=e^{{frac {i}{hbar }}mathbf {p} .mathbf {r} }e^{-{frac {i}{hbar }}Et}}

*

Với Ψ {displaystyle Psi } là hàm sóng của hạt. Bước sóng được tính bằng bước sóng de Broglie λ = h p {displaystyle lambda ={frac {h}{p}}} Tần số của hàm sóng cũng liên hệ với năng lượng của hạt, tương tự như trường hợp của photon, là: f = E h {displaystyle f={frac {E}{h}}}

*

Năng lượng sóng lượng tử E = h f {displaystyle E=hf} ===Phương trình Schrodinger=== Phương trình Schrodinger là một phương trình tính toán lượng tử dùng để mô tả chuyển động của quang tuyến trong nguyên tử .Phương trình Schrodinger được áp dung trong nhửng trường hợp hạt chuyển động nhanh so với tốc độ ánh sáng, theo tên của Erwin Schrödinger, người đã lần đầu tiên thiết lập nó vào năm 1926 Sự biến đổi của hàm sóng theo thời gian hoàn toàn được xác định thông qua phương trình Schodinger. Cho một trường thế năng mà một hệ vật chất chuyển động bên trong, có thể giải phuơng trình Schrodinger để thu được hàm sóng thỏa mãn, và từ hàm sóng có thể xác định các đại lượng vật lý của hệ vật chất đang quan tâm. Phương trình Schrodinger do đó đóng một vai trò quan trọng trong cơ học lượng tử, tuơng tự như vai trò của phương trình chuyển động trong định luật hai Newton đối với cơ học cổ điển. Với một hệ vật chất chuyển động trong một tầng điện năng có năng lượng E tính bằng tổng của động năng , K , và điện năng , P E = K + P {displaystyle E=K+P}

*

E ^ = K ^ + P ^ {displaystyle {hat {E}}={hat {K}}+{hat {P}}}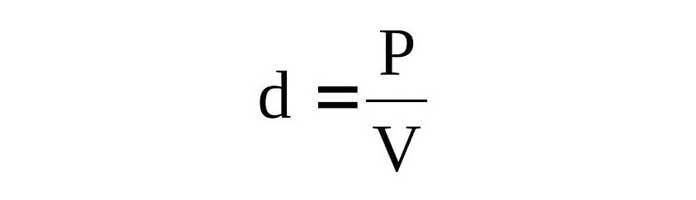

*

i ℏ ∂ ∂ t = − ℏ 2 2 m ∇ 2 + V ( r ) {displaystyle ihbar {frac {partial }{partial t}}={frac {-hbar ^{2}}{2m}}
abla ^{2}+V(mathbf {r} )}

*

và, khi tác động toán tử ở hai vế lên hàm sóng Ψ {displaystyle Psi } : E ^ Ψ = ( K ^ + P ^ ) Ψ {displaystyle {hat {E}}Psi =({hat {K}}+{hat {P}})Psi }

*

i ℏ ∂ ∂ t Ψ = ( − ℏ 2 2 m ∇ 2 + V ( r ) ) Ψ {displaystyle ihbar {frac {partial }{partial t}}Psi =({frac {-hbar ^{2}}{2m}}
abla ^{2}+V(mathbf {r} ))Psi } i ℏ ∂ ∂ t Ψ = H ^ Ψ {displaystyle ihbar {frac {partial }{partial t}}Psi ={hat {H}}Psi } Phương trình Schrodinger có công thức tổng quát sauPhương trình Schrodinger không phụ thuộc thời gian i ℏ ∂ ∂ t Ψ = ( − ℏ 2 2 m ∇ 2 + V ( r ) ) Ψ {displaystyle ihbar {frac {partial }{partial t}}Psi =({frac {-hbar ^{2}}{2m}}
abla ^{2}+V(mathbf {r} ))Psi } i ℏ ∂ ∂ t Ψ = H ^ Ψ {displaystyle ihbar {frac {partial }{partial t}}Psi ={hat {H}}Psi } Với H ^ = − ℏ 2 2 m ∇ 2 + V ( r ) {displaystyle {hat {H}}={frac {-hbar ^{2}}{2m}}
abla ^{2}+V(mathbf {r} )}

*

Phương trình Schrodinger phụ thuộc thời gian i ℏ ∂ ∂ t Ψ = ( − ℏ 2 2 m ∇ 2 + V ( r , t ) ) Ψ {displaystyle ihbar {frac {partial }{partial t}}Psi =({frac {-hbar ^{2}}{2m}}
abla ^{2}+V(mathbf {r} ,t))Psi }

*

i ℏ ∂ ∂ t Ψ = H ^ Ψ {displaystyle ihbar {frac {partial }{partial t}}Psi ={hat {H}}Psi } Với H ^ = − ℏ 2 2 m ∇ 2 + V ( r , t ) {displaystyle {hat {H}}={frac {-hbar ^{2}}{2m}}
abla ^{2}+V(mathbf {r} ,t)}

*

Toán tử Hamilton có ký hiệu H ^ {displaystyle {hat {H}}}

*

H ^ = ( − ℏ 2 2 m ∇ 2 + V ( r ) ) {displaystyle {hat {H}}=({frac {-hbar ^{2}}{2m}}
abla ^{2}+V(mathbf {r} ))}

*

. Hệ toán không phụ thuộc thời gian H ^ = ( − ℏ 2 2 m ∇ 2 + V ( r , t ) ) {displaystyle {hat {H}}=({frac {-hbar ^{2}}{2m}}
abla ^{2}+V(mathbf {r,t} ))}

*

. Hệ toán phụ thuộc thời gian

Chuyên mục: Hỏi Đáp

.tags a {
color: #fff;
background: #909295;
padding: 3px 10px;
border-radius: 10px;
font-size: 13px;
line-height: 30px;
white-space: nowrap;
}
.tags a:hover { background: #818182; }

#footer {font-size: 14px;background: #ffffff;padding: 10px;text-align: center;}
#footer a {color: #2c2b2b;margin-right: 10px;}