Ngoại suy là gì

Sự khác biệt giữa ngoại suy và nội suy là gì, và cách chính xác nhất để sử dụng các thuật ngữ này là gì?

Ví dụ, tôi đã thấy một tuyên bố trong một bài báo sử dụng phép nội suy như:

“Quy trình nội suy hình dạng của hàm ước tính giữa các điểm bin”

Một câu sử dụng cả phép ngoại suy và phép nội suy là, ví dụ:

Bước trước đó, chúng tôi ngoại suy hàm nội suy bằng phương thức Kernel ở đuôi nhiệt độ bên trái và bên phải.

Bạn đang xem: Ngoại suy là gì

Ai đó có thể cung cấp một cách rõ ràng và dễ dàng để phân biệt chúng và hướng dẫn cách sử dụng các thuật ngữ này một cách chính xác với một ví dụ không?

terminology interpolation extrapolation
— Frank Swanton nguồn
1
Một câu hỏi liên quan.
— JM không phải là một nhà thống kê
1
Có thể trùng lặp Điều gì là sai với phép ngoại suy?
— usεr11852 nói Phục hồi Monic
usεr11852 Tôi nghĩ rằng hai câu hỏi bao gồm mặt bằng tương tự nhưng khác nhau bởi vì câu hỏi này yêu cầu sự tương phản với nội suy.
— mkt – Phục hồi
Sự khác biệt giữa phép nội suy và phép ngoại suy này đã được chính thức hóa một cách chặt chẽ theo cách đã được thống nhất chung, (ví dụ, thông qua vỏ tàu lồi) hay những thuật ngữ này vẫn phải chịu sự phán xét và giải thích của con người?
— Nick Alger

Câu trả lời:

Để thêm một lời giải thích trực quan cho điều này: hãy xem xét một vài điểm mà bạn dự định làm mô hình.

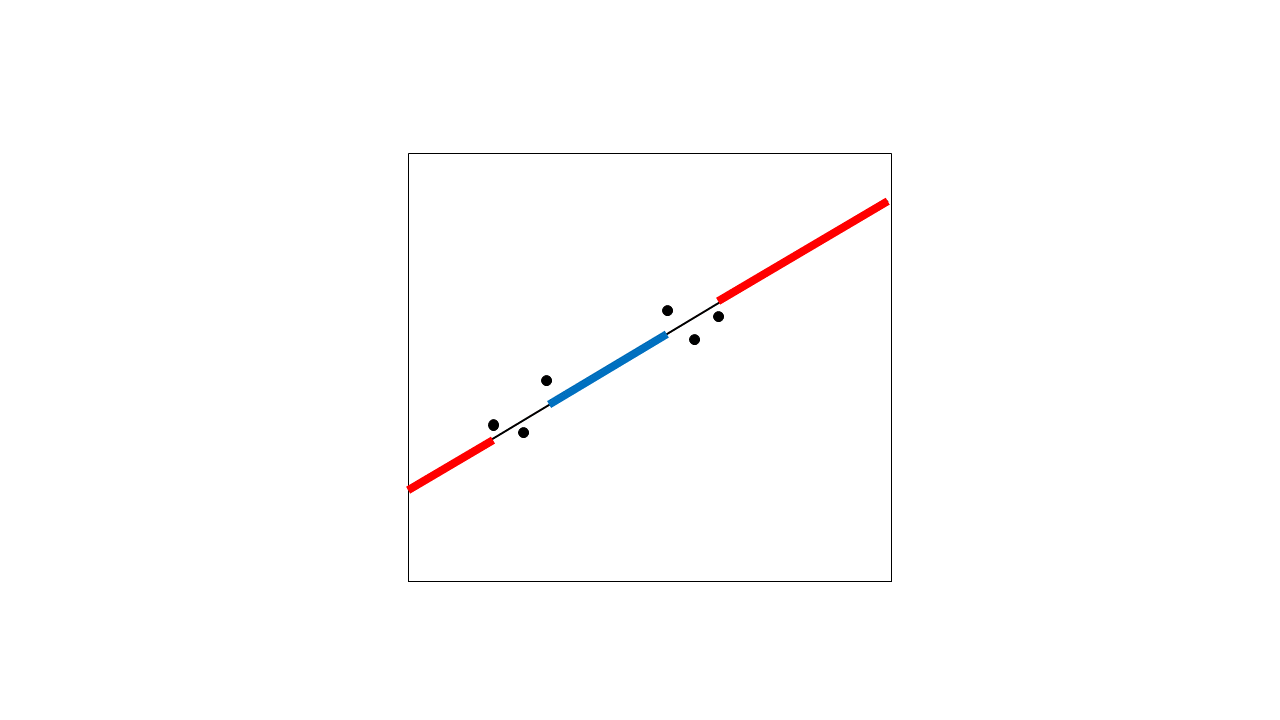
Chúng trông giống như chúng có thể được mô tả tốt với một đường thẳng, vì vậy bạn phù hợp với hồi quy tuyến tính với chúng:

Đường hồi quy này cho phép bạn cả nội suy (tạo các giá trị dự kiến ở giữa các điểm dữ liệu của bạn) và ngoại suy (tạo các giá trị dự kiến nằm ngoài phạm vi của các điểm dữ liệu của bạn). Tôi đã nhấn mạnh phép ngoại suy màu đỏ và vùng nội suy lớn nhất màu xanh lam. Để rõ ràng, ngay cả các vùng nhỏ giữa các điểm cũng được nội suy, nhưng tôi chỉ làm nổi bật vùng lớn ở đây.

Tại sao ngoại suy nói chung là một mối quan tâm nhiều hơn? Bởi vì bạn thường ít chắc chắn hơn về hình dạng của mối quan hệ ngoài phạm vi dữ liệu của bạn. Xem xét những gì có thể xảy ra khi bạn thu thập thêm một vài điểm dữ liệu (vòng tròn rỗng):

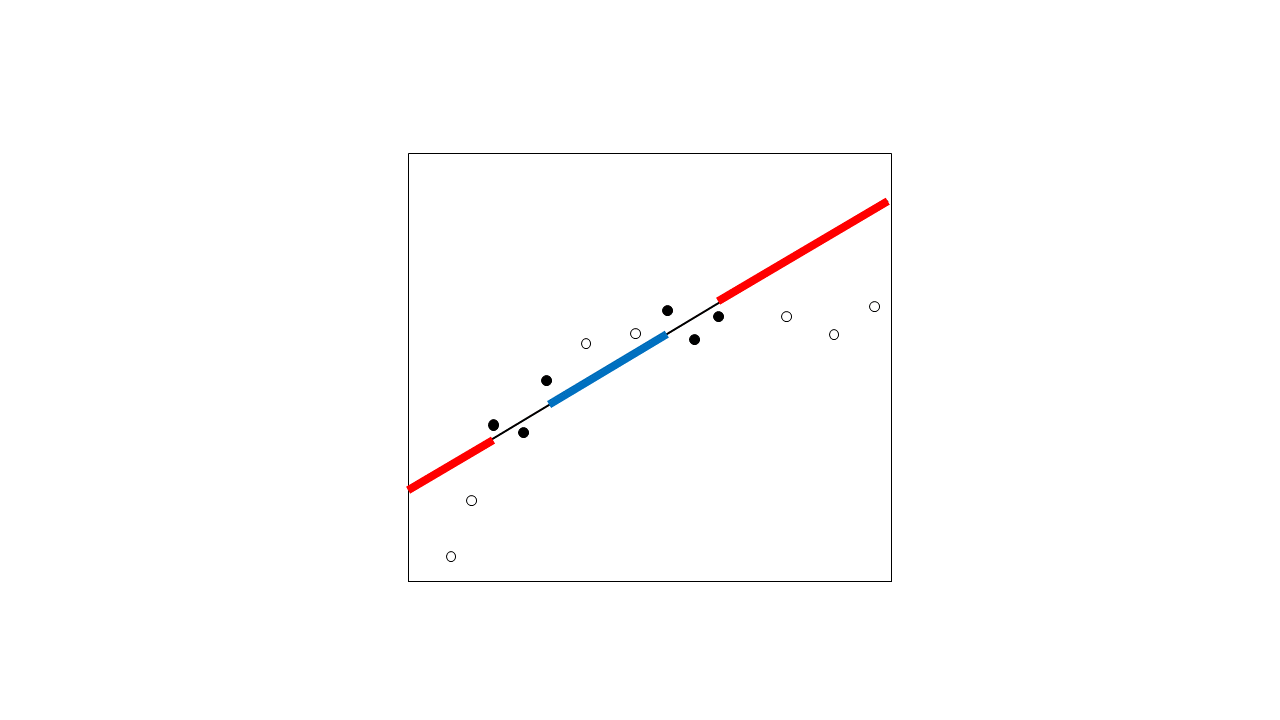
Nó chỉ ra rằng mối quan hệ đã không được nắm bắt tốt với mối quan hệ giả định của bạn sau khi tất cả. Các dự đoán trong khu vực ngoại suy đang tắt. Ngay cả khi bạn đã đoán đúng chức năng mô tả chính xác mối quan hệ phi tuyến tính này, dữ liệu của bạn không mở rộng đủ phạm vi để bạn nắm bắt tốt tính phi tuyến, do đó bạn vẫn có thể ở khá xa. Lưu ý rằng đây là một vấn đề không chỉ đối với hồi quy tuyến tính, mà đối với bất kỳ mối quan hệ nào – đây là lý do tại sao phép ngoại suy được coi là nguy hiểm.

Xem thêm: Representation Là Gì – Nghĩa Của Từ Representation

Dự đoán trong khu vực nội suy cũng không chính xác vì thiếu tính phi tuyến trong sự phù hợp, nhưng lỗi dự đoán của chúng thấp hơn nhiều. Không có gì đảm bảo rằng bạn sẽ không có mối quan hệ bất ngờ ở giữa các điểm của bạn (tức là khu vực nội suy), nhưng nói chung là ít có khả năng hơn.

Tôi sẽ nói thêm rằng phép ngoại suy không phải lúc nào cũng là một ý tưởng tồi tệ – nếu bạn ngoại suy một chút nhỏ ngoài phạm vi dữ liệu của mình, có lẽ bạn sẽ không sai lắm (mặc dù điều đó là có thể!). Người cổ đại không có mô hình khoa học tốt về thế giới sẽ không sai lầm nếu họ dự đoán rằng mặt trời sẽ mọc lại vào ngày hôm sau và ngày hôm sau (mặc dù một ngày nữa trong tương lai, thậm chí điều này sẽ thất bại).

Xem thêm: Yý Thức Là Gì – Khái Niệm Về ý Thức

2″ role=”presentation”>22

Chỉnh sửa dựa trên các nhận xét: cho dù nội suy hay ngoại suy, tốt nhất là luôn có một số lý thuyết để kỳ vọng nền tảng. Nếu mô hình hóa lý thuyết phải được thực hiện, rủi ro từ phép nội suy thường ít hơn so với phép ngoại suy. Điều đó nói rằng, khi khoảng cách giữa các điểm dữ liệu tăng cường độ, phép nội suy cũng ngày càng trở nên nguy hiểm hơn.

Chuyên mục: Hỏi Đáp