Author Bài viết Bài giảng Giải tích 1 Hàm số – Hàm lượng giác ngược – Hàm hyperbol Chia một đa thức cho tam thức bậc 2 Giới hạn của hàm số (Limit of a function) Vô cùng bé (infinitesimal) Đạo hàm và vi phân của hàm số (derivative and differential of a function) Khai triển Taylor – Maclaurin (Taylor expansion) Khảo sát đường cong tham số Tích phân hữu tỷ (integration by partial fractions) Tích phân hàm vô tỉ (Integrals involving roots) Tích phân suy rộng (Improper Integrals) Chuỗi số. Tổng của chuỗi (Series. The total sum of series) Chuỗi số dương (Infinitive Series) Chuỗi Fourier Chuỗi Fourier Sine và Cosine Giải tích 2 Khái niệm mở đầu về hàm nhiều biến Giới hạn của hàm hai biến số Đạo hàm riêng Hàm số khả vi và vi phân toàn phần Đạo hàm của hàm hợp Đạo hàm hàm số ẩn Cực trị (không điều kiện) của hàm 2 biến Cực trị có điều kiện (cực trị ràng buộc) Các khái niệm cơ bản của phương trình vi phân Phương trình tách biến, phương trình đẳng cấp cấp 1 Phương trình vi phân tuyến tính cấp 1, Bernoulli, Ricatti Phương trình vi phân tuyến tính cấp 2 (linear second-order ordinary differential equation) Ứng dụng chuỗi số giải phương trình vi phân Tích phân hai lớp (Tích phân kép) Tích phân hai lớp trong tọa độ cực. Công thức đổi biến Tích phân đường theo tọa độ (Tp đường loại 2) Số phức (Complex Number) Đại số tuyến tính (Linear Algebra) Tập hợp Khái niệm về ma trận Ma trận bậc thang (Echelon matrix) Ma trận nghịch đảo (khả nghịch) Thuật toán tìm ma trận bậc thang Định thức (Determinants) Hệ phương trình tuyến tính (System of Linear Equations) Khái niệm về ánh xạ tuyến tính Không gian vectơ Euclide (Euclidean Vector Spaces) Trị riêng, vectơ riêng của ma trận (Eigenvalues and Eigenvectors) Dạng toàn phương Xác suất thống kê Bổ túc về Giải tích Tổ hợp Biến cố và quan hệ giữa các biến cố Các định nghĩa của xác suất Xác suất có điều kiện Đại lượng ngẫu nhiên 1 chiều Một số quy luật phân phối xác suất rời rạc Ước lượng tham số của tổng thể Kiểm định giả thiết Phương pháp Toán Lý (PT Đạo hàm riêng và PBĐ Laplace) Phép biến đổi Laplace – Các khái niệm mở đầu Bài tập Trắc nghiệm Thảo luận Thảo luận (tiếp theo) Thảo luận chung (tt) Thảo luận về giải tích Thảo luận Giải tích – Trang 2 Thảo luận ĐSTT Trang 2 Trang 3 Thảo luận XSTK Trang 2 Thảo luận về tích phân bội Đề thi Ebooks Maths Ebooks Giải tích – Đại số XSTK – Phương pháp tính Hàm phức – PDEs Tài liệu khác Giáo dục – Khoa học Thư giãn Một thời để nhớ Softwares Links Sitemap
Trị riêng, vectơ riêng của ma trận (Eigenvalues and Eigenvectors)
Shortlink: http://wp.me/P8gtr-tp
I. Trị riêng, vectơ riêng:
1.1 Định nghĩa : Cho A là ma trận vuông cấp n trên trường số
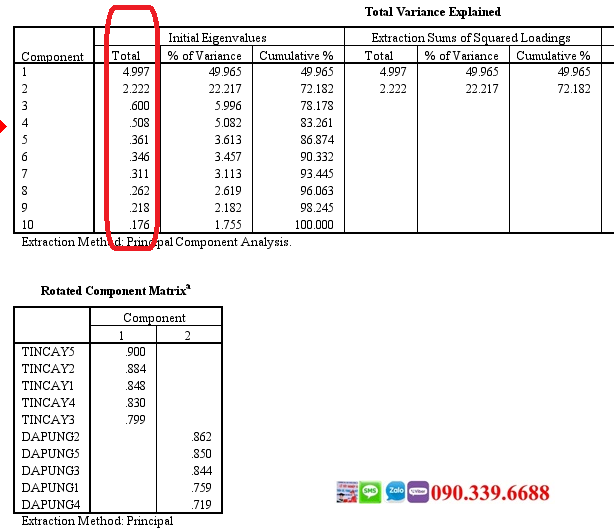
. Số
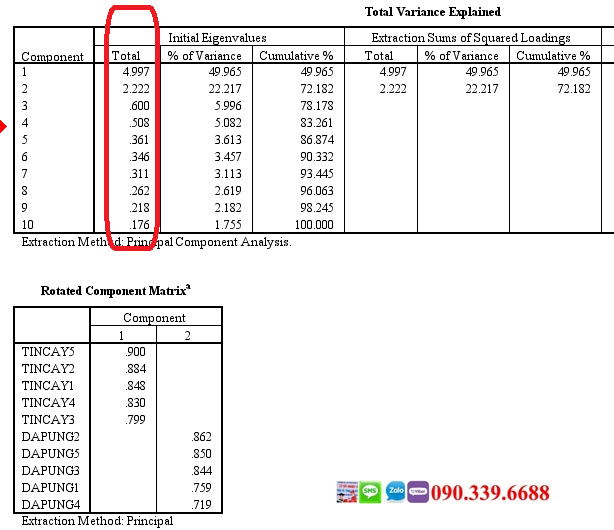
được gọi là giá trị riêng (gọi tắt là trị riêng – kí hiệu GTR) của ma trận A, nếu tồn tại một vectơ
sao cho:
Khi đó vectơ u được gọi là vectơ riêng (VTR) của ma trận A ứng với giá trị riêng
1.2 Tính chất:
1. Giá trị riêng

chính là nghiệm của phương trình $latex det(A-I) = 0 &fg=ff0000$ (1) được gọi là phương trình đặc trưng của ma trận A.
Bạn đang xem: Eigenvalues là gì
2. Một giá trị riêng có thể có nhiều vectơ riêng.
3. Mỗi vectơ riêng chỉ ứng với một giá trị riêng duy nhất.
4. Ma trận A là nghiệm của đa thức đặc trưng của chính nó (trong trường hợp này đa thức đặc trưng được coi là đa thức ma trận, nghĩa là biến số của nó không phải là biến số thực mà là biến ma trận)
5. Nếu
là giá trị riêng của ma trận A thì A không khả nghịch. Ngược lại, nếu mọi GTR của A đều khác không thì A khả nghịch.
6. Nếu
là GTR của ma trận A thì
là giá trị riêng của ma trận
Chứng minh :
1. Số

là trị riêng của A khi và chỉ khi
. Suy ra: hệ phương trình tuyến tính thuần nhất
có nghiệm
.
2. Điều này là hiển nhiên vì dựa vào định nghĩa và tính chất 1 thì hệ phương trình

có vô số nghiệm.
3. Giả sử vectơ riêng
ứng với 2 trị riêng
.
Ta cần chứng minh:

. Thật vậy, ta có :

Mà:

. Do đó:

◊
4. Ta có:
5. Do

là GTR của ma trận A. Do đó:
.
Chứng tỏ A suy biến (không khả nghịch).
6. Ta có

. Do đó:
.
Xem thêm: Ddos Là Gì – Hệ Thống Chống Ddos Anti Ddos
Từ đó, bằng cách chứng minh quy nạp, bạn sẽ có kết quả.
Nhận xét: từ kết quả trên, ta nhận thấy có 1 cách để tính nhanh
. Đó là ta tìm đa thức đặc trưng
của ma trận A. Sau đó, tính giá trị của P(a).
1.3. Phương pháp giải tìm trị riêng, vectơ riêng:
Bước 1: Giải phương trình đặc trựng
tìm giá trị riêng.
Bước 2: Tìm vectơ riêng ứng với giá trị riêng

:
Ứng với mỗi giá trị riêng

vừa tìm được, ta giải hệ phương trình tuyến tính thuần nhất
Lưu ý : theo tính chất trên, thì hpt (2) luôn luôn có vô số nghiệm. Do đó, nếu bạn giải pt (2) mà vô nghiệm hoặc có nghiệm duy nhất thì phải kiểm tra lại.
1.4 Không gian con riêng ứng với GTR

Các vetơ riêng của ma trận A ứng với giá trị riêng
cùng với vectơ 0 tạo thành 1 không gian con được gọi là không gian con riêng ứng với

.
Ký hiệu:

Nếu giá trị riêng

là nghiệm bội k thì
1.5 Các ví dụ :
Ví dụ 1 . Tìm GTR, VTR của ma trận A:
” title=”left ” class=”latex” />
Bước 1: Lập phương trình đặc trưng của ma trận A:

Giải phương trình đặc trưng, ta có:

Bước 2: Tìm các VTR:
1. Ta tìm các VTR ứng với giá trị riêng

Ứng với giá trị riêng

ta có VTR
là nghiệm của hệ phương trình:
Vậy VTR ứng với GTR

có dạng

2. Ta tìm các VTR ứng với giá trị riêng
Ứng với giá trị riêng

ta có VTR
là nghiệm của hệ phương trình:
Vậy VTR ứng với GTR

có dạng
Ví dụ 2: Tìm GTR, VTR của ma trận A:
” title=”left ” class=”latex” /> , xem A là ma trận phức
Bước 1: Lập phương trình đặc trưng của ma trận A:
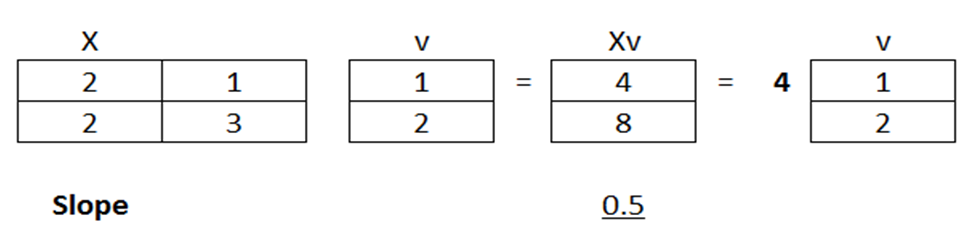
Phương trình (1) vô nghiệm thực. Tuy nhiên do A là ma trận phức nên ta tìm GTR phức của ma trận. Giải phương trình đặc trưng, ta có:

Bước 2: Tìm các VTR:
1. Ta tìm các VTR ứng với giá trị riêng

Ứng với giá trị riêng

ta có VTR

là nghiệm của hệ phương trình:
Vậy VTR ứng với GTR

có dạng

2. Ta tìm các VTR ứng với giá trị riêng

Ứng với giá trị riêng

ta có VTR
là nghiệm của hệ phương trình:
Vậy VTR ứng với GTR
có dạng
Ví dụ 3 :
a. Tìm đa thức đặc trưng của ma trận:
” title=”A = left ” class=”latex” />
b. Dựa vào đa thức đặc trưng, chứng minh A khả nghịch và chỉ ra biểu thức xác định

c. Tính

d. Tìm GTR, VTR của A.
Giải.
a. Tương tự như các ví dụ trên, ta dễ dàng tìm được đa thức đặc trưng của ma trận A:

b. Theo tính chất 4 ta có:

. Do đó:

Đặt
.
Xem thêm: Tải Game Gata – Download Game Gta Vice City Full
Ta có:
.
Do đó: A khả nghịch và

c. Ta có

nên:

d. Từ đa thức đặc trưng ta tìm được các GTR:

Khi đó: VTR ứng với giá trị riêng
có dạng:

VTR ứng với giá trị riêng

có dạng:

VTR ứng với giá trị riêng
có dạng:
Chuyên mục: Hỏi Đáp