Lý thuyết chung về đa thức và tài liệu ôn thi hay nhất
Trongtoán học,đa thức là một phần lý thuyết cơ bản quan trọng mà các bạn đã được tiếp xúc từ rất sớm, đa thức trên một vành (hoặc trường)Klà một biểu thức dưới dạng tổng đại số của các đơn thức. Bài học ngày hôm nay chúng ta sẽ cùng nhau tìm hiểu về những lý thuyết chung nhất về đa thức nhằm hiểu rõ bản chất của khái niệm này nhé. Mời các bạn cùng theo dõi!
I. Khái niệm về đa thức
Đa thức là gì?
Trong chương trìnhgiáo dục phổ thông, thường xét các đa thức trên trường số thực, trong những bài toán cụ thể có thể xét các đa thức với hệ số nguyên hoặc hệ số hữu tỷ.
Bạn đang xem: đa thức là gì
Cụ thể(f (x, y, z) = ax+by+cz)được coi là một đa thức, vớix,yvàzlà các biến.
Hàm số biểu diễn bởi một đa thức được gọi là hàm đa thức. Phương trìnhP= 0 trong đóPlà một đa thức được gọi là phương trình đại số.
Nghiệm của đa thức?
Các bài toán đầu tiên về đa thức là tìm các nghiệm của đa thức, cũng là nghiệm của phương trình đại số vì nếu ta có x là nghiệm của đa thức f(x) làm cho đa thức này bằng không,do đó x là nghiệm của phương trình f(x).
Ví dụ: Tìm nghiệm của đa thức sau đây:
(x^3+2x^2-x-2=0)
(leftrightarrow (x^3+2x^2)-(x+2)=0)
(leftrightarrow x^2(x+2)-(x+2)=0)
(leftrightarrow (x^2-1)(x+2)=0)
(leftrightarrow left{egin{array}{cc}x^2-1=0leftrightarrow x^2=1leftrightarrow x=+-1x+2=0leftrightarrow x=-2end{array}
ight.)
Vậy phương trình có ba nghiệm là x = {-2; -1; 1}.
Xem thêm: silent là gì
Biến?
Cho(F(x)=(x_1,x_2,…,x_m)), ta gọi x là biến của phương trình F(x) hay còn nóiF(x) có m biến x.
II. Cộng trừ đa thức
Công đa thức
Muốn cộng hai đa thức ta có thể lần lượt thực hiện các bước:
Viết liên tiếp các hạng tử của hai đa thức đó cùng với dấu của chúng. Thu gọn các hạng tử đồng dạng (nếu có).
Trừ đa thức
Muốn trừ hai đa thức ta có thể lần lượt thực hiện các bước:
Viết các hạng tử của đa thức thứ nhất cùng với dấu của chúng. Viết tiếp các hạng tử của đa thức thứ hai với dấu ngược lại. Thu gọn các hạng tử đồng dạng (nếu có).
III. Nhân chia đa thức
Nhân đơn thức với đa thức
Ta thực hiện nhân đơn thức với từng hạng tử của đa thức sau đó cộng tổng lại với nhau.
Công thức:(A(B+C)=AB+BC)
Ví dụ:(x(2x+1)=2x^2+x)
Tham khảo thêm tài liệuNhân đơn thức với đa thức
Nhân đa thức với đa thức
Ta thực hiện nhân lần lượt từng hạng tử của đa thức này với các hạng tử của đa thức kia, sau đó cộng tổng lại với nhau
Công thức:((A+B)(C+D)=AC+AD+BC+BD)
Ví dụ:((x+1)(x-2)=x^2-2x+x-2=x^2-x-2)
Tham khảo thêm tài liệuNhân đa thức với đa thức
Chia đa thức cho đơn thức
Ta thực hiện chia lần lượt từng hạng tử của đa thức cho đơn thức sau đó cộng tổng lại với nhau. Để hiểu rõ hơn mời bạn tham khảo ví dụ sau đây:
Ví dụ: Rút gọn biểu thức:((a^2b−3ab^2):(dfrac{1}{2}ab)+(6b^3−5ab^2):b^2.)((a^2b−3ab^2):(dfrac{1}{2}ab)+(6b^3−5ab^2):b^2 =2a−6b+6b−5a=−3a.)
Tham khảo thêm tài liệuChia đa thức với đơn thức
Chia đa thức cho đa thức
Ta thực hiện sắp xếpđa thức theo lũy thừa giảm dần của biến, sau đó thực hiện phép chia. Để hiểu rõ hơn về phương pháp làm mời các bạn tham khảo ví dụ sau đây:
Ví dụ:((2x^4−3x^3−3x^2−2+6x):(x^2−2))
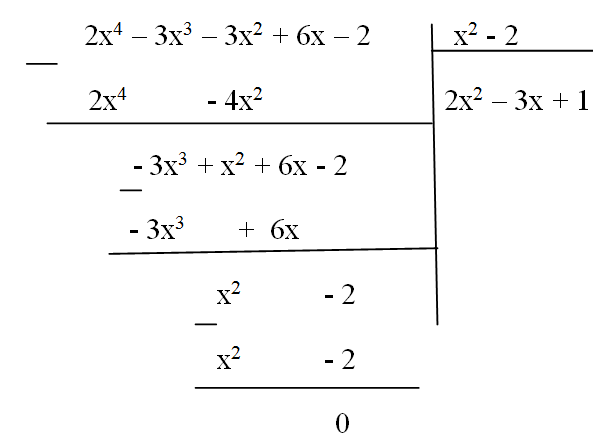
Chia đa thức cho một biến đã sắp xếp
Ta trình bày phép chia tương tự như cách chia các số tự nhiên.
– Sắp xếpđa thức theo lũy thừa giảm dần của biến.
Xem thêm: Tải Game Phiêu Lưu – Game Phiêu Lưu Commando Cho Android
– Áp dụng qui tắc chia hai đa thức 1 biến đã sắp xếp.
Ví dụ:((x^3−7x+3−x^2):(x−3))
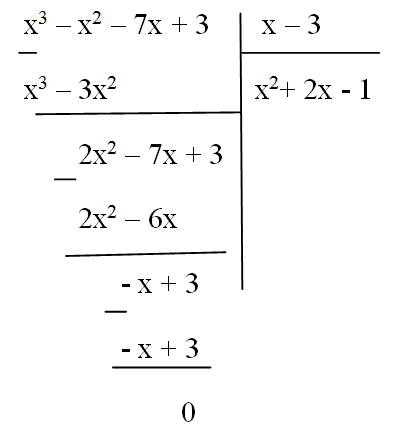
Để luyện tập thêm các bài tập dạng này bạn có thể tham khảo thêm các bài tập đã có lời giải sau đây:Chia đa thức một biến đã sắp xếp
IV. Phân tích đa thức thành nhân tử bằng phương pháp đặt nhân tử chung
Phân tích đa thức thành nhân tử bằng phương pháp đặt nhân tử chung là biến đổi đa thức đó thành tích của những đa thức
Phương pháp đặt nhân tử chung là một phương pháp phân tích đa thức thành nhân tử bảng cách nhóm các hạng tử có chung nhân tử với nhau.(AB+AC=A(B+C))
Bài tập: Phân tích các đa thức sau đây thành nhân tử:
a) (x^2 – x)
b) (5x^2(x – 2y) – 15x(x – 2y))
c) (3(x – y) – 5x(y – x))
Hướng dẫn giải
a) (x^2 – x = x.x – x.1 = x(x – 1))
b)(5x^2 (x – 2y)– 15x(x – 2y) = x.5x(x – 2y) – 3.5x(x – 2y) = (x – 3).5x(x – 2y))
c)(3(x – y)– 5x(y – x) = 3(x – y) + 5x(x – y) = (3 + 5x)(x – y))
Tham khảo thêm các bài tập liên quan tạiPhân tích đa thức thành nhân tử bằng phương pháp đặt nhân tử chung
Hy vọng rằng những kiến thức tổng hợp trên sẽ giúp bạn hình dung rõ ràng lý thuyết về đa thức và cácphương pháp làm các dạngbài tập liên quan. Ngoài ra để củng cố thêm việc học các bạn nên dành thời gian để luyện tập thêm nhằmghi nhớ các công thức cần thiết. Chúc các bạn thành công!
Chuyên mục: Hỏi Đáp