Cực trị của hàm số là gì? Cực trị của hàm số bậc 3, bậc 4, cực trị của hàm số lượng giác, cực trị của hàm số logarit… là những kiến thức Đại số khá thú vị và cần thiết để các em học sinh Trung học Phổ thông chú ý. Sau đây thienmaonline.vn sẽ chia sẻ một số thông tin cơ bản về các loại cực trị của hàm số.
Bạn đang xem: Cực trị là gì
Cực trị của hàm số là gì?
Cho hàm số y = f(x) liên tục trên khoảng (a; b) và điểm x0 ∈ (a; b).
Nếu tồn tại số h > 0 sao cho f(x) 0), ∀x ∈ (x0 – h ; x0 + h), x ≠ x0 thì ta nói hàm số f đạt cực đại tại x0 .Nếu tồn tại số h > 0 sao cho f(x) > f(x0), ∀x ∈ (x0 – h ; x0 + h), x ≠ x0 thì ta nói hàm số f đạt cực tiểu tại x0 .
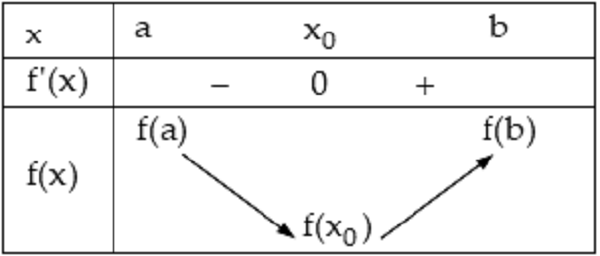
Định lý 1: Cho hàm số y = f(x) liên tục trên khoảng K = (x0 – h ; x0 + h) (h > 0) và có đạo hàm trên K hoặc trên K ∖{ x0 }.
Nếu (left { f”(x)> 0mid forall (x_{0}-h; x_{0})f”(x) thì (x_{0}) là điểm cực đại của hàm số.Nếu (left { f”(x)> 0mid forall (x_{0}-h; x_{0})f”(x) thì (x_{0}) là điểm cực tiểu của hàm số.
Định lý 2. Cho hàm số y = f(x) có đạo hàm cấp hai trên khoảng K = (x0 – h; x0 + h) (h > 0).
Nếu f”(x0) = 0, f”(x0) > 0 thì x0 là điểm cực tiểu của hàm số f.Nếu f”(x0) = 0, f”(x0) 0 là điểm cực đại của hàm số f.
Cực trị của hàm số bậc 3, bậc 4
Cực trị của hàm số bậc 3
Cho hàm số: (y = f(x) = ax^{3} + bx^{2} + cx + d (a
eq 0))
Đạo hàm: (y’= f’(x) = 3ax^{2} + 2bx + c)
Điều kiện tồn tại cực trị: y = f(x) có cực trị y = f(x) có cực đại và cực tiểu.
Xem thêm: điều Lệ Công Ty Tiếng Anh Là Gì, Bản Dịch điều Lệ Công Ty Tiếng Anh
=> f’(x) = 0 có 2 nghiệm phân biệt (Delta ‘=b^{2}-3ac> 0)
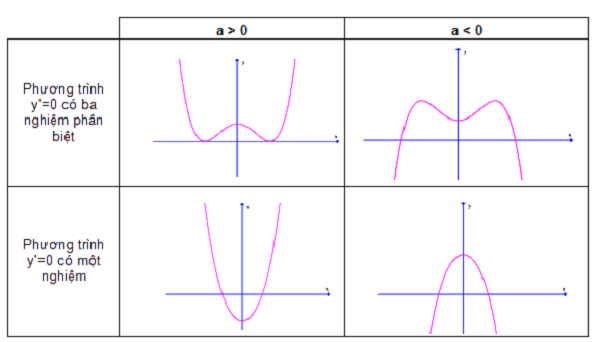
Cực trị của hàm số bậc 4 (hàm trùng phương)
Cho hàm số: (y=f(x)=ax^{4}+bx^{3}+cx^{2}+dx+e (a
eq 0))
Đạo hàm: (y’=f”(x)=4ax^{3}+3bx^{2}+2cx+d)
Cực trị:
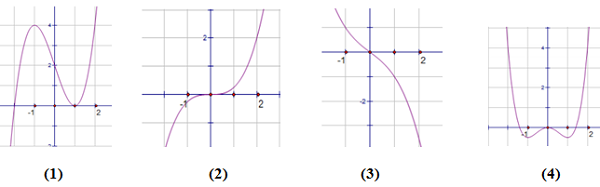
Xét f’(x)=0 => Có 3 trường hợp xảy ra:
TH1: có đúng 1 nghiệm => có đúng 1 cực trị.TH2: có đúng 2 nghiệm: 1 nghiệm đơn và 1 nghiệm kép =>có đúng 1 cực trị.TH3: có 3 nghiệm phân biệt => có 3 cực trị gồm cực đại và cực tiểu.
Cực trị của hàm số lượng giác
Phương pháp tìm cực trị của hàm số lượng giác như sau:
Bước 1: Tìm miền xác định của hàm số.Bước 2: Tính đạo hàm y’ = f’(x), giải phương trình y’=0, giả sử có nghiệm x=x0.Bước 3: Khi đó: Tìm đạo hàm y’’.Tính y’’(x0) rồi đưa ra kết luận dựa vào định lý 2.
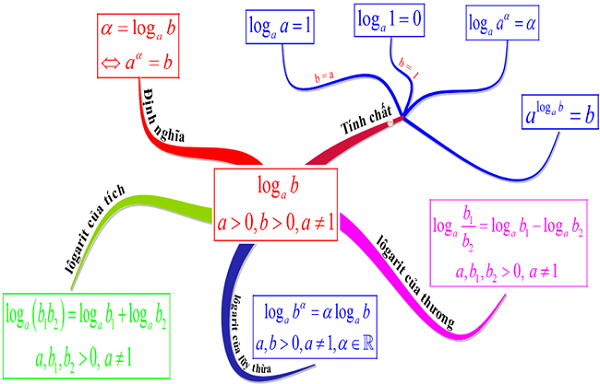
Cực trị của hàm số logarit
Chúng ta thực hiện theo các bước sau:
Bước 1: Tìm miền xác định của hàm số.
Bước 2: Tính đạo hàm y’, rồi giải phương trình y’=0, giả sử có nghiệm x=x0.
Bước 3: Xét hai khả năng:
Nếu xét được dấu của y’: Khi đó: lập bảng biến thiên rồi đưa ra kết luận dựa vào định lý 2.Nếu không xét được dấu của y’: Khi đó:Tìm đạo hàm y’’.Tính y’’(x0) rồi đưa ra kết luận dựa vào định lý 3.
Xem thêm: Tự Luyến Là Gì – Bệnh Tự Luyến Có Nguy Hiểm Không
Ví dụ minh họa cực trị của hàm số là gì?
Tìm cực trị của hàm số: (y=xe^{-3x})
Ta có: (y’= e^{-3x}-3xe^{-3x}=e^{-3x}(1-3x))
(Rightarrow y’=0Leftrightarrow 1-3x=0Leftrightarrow x=frac{1}{3})
Ta lại có: (y”=-3e^{-3x}-3(1-3x)e^{-3x})
Thay (x=frac{1}{3}) vào y’’ và được (y”(frac{1}{3})
Vậy hàm số đã cho có điểm cực đại là (x=frac{1}{3}).
Hy vọng bài viết trên đây đã cung cấp cho bạn những thông tin cần thiết cũng như kiến thức bổ ích về cực trị của hàm số là gì, cực trị của hàm số bậc 3 và bậc 4, cực trị của hàm số lượng giác hay cực trị của hàm số logarit. Nếu có băn khoăn nào, mời bạn để lại nhận xét bên dưới bài viết “Cực trị của hàm số là gì” để chúng mình cùng nhau trao đổi thêm nhé!
Xem chi tiết qua bài giảng dưới đây:
Chuyên mục: Hỏi Đáp