Đôi khi tôi thấy (n) với biểu tượng strange lạ với một cái gì đó ở giữa nó, và đôi khi chỉ là O (n). Có phải chỉ là sự lười biếng khi gõ bởi vì không ai biết cách gõ biểu tượng này, hoặc nó có nghĩa gì đó khác nhau?
Giải thích ngắn gọn:
Nếu một thuật toán là (g (n)), điều đó có nghĩa là thời gian chạy của thuật toán khi n (kích thước đầu vào) lớn hơn tỷ lệ với g (n).
Bạn đang xem: Big o notation là gì
Nếu một thuật toán là O (g (n)), điều đó có nghĩa là thời gian chạy của thuật toán khi n lớn hơn là nhất tỷ lệ với g (n).
Thông thường, ngay cả khi mọi người nói về O(g(n)) họ thực sự có nghĩa là Θ (g (n)) nhưng về mặt kỹ thuật, có một sự khác biệt.
Kỹ thuật hơn:
O (n) đại diện cho giới hạn trên. (N) có nghĩa là ràng buộc chặt chẽ. (N) đại diện cho giới hạn dưới.
f(x) = Θ(g(x)) iff f(x) = O(g(x)) and f(x) = Ω(g(x))
Về cơ bản khi chúng ta nói một thuật toán là O (n), thì đó cũng là O (n2), Trên1000000), O (2n), … nhưng thuật toán Θ (n) là không (n2).
Trong thực tế, vì f(n) = (g (n)) có nghĩa là cho các giá trị đủ lớn của n, f(n) có thể được ràng buộc trong c1g (n) và c2g (n) cho một số giá trị của c1 và C2, tức là tốc độ tăng trưởng của f không có triệu chứng bằng g: g có thể là giới hạn dưới và và giới hạn trên của f. Điều này trực tiếp ngụ ý f có thể là giới hạn dưới và giới hạn trên của g là tốt. Hậu quả là,
f(x) = Θ(g(x)) iff g(x) = Θ(f(x))
Tương tự, để hiển thị f(n) = (g (n)), đủ để hiển thị g là giới hạn trên của f (tức là f(n) = O(g(n))) và f là giới hạn dưới của g (tức là f(n) = Ω (g (n)) giống hệt như g(n) = O (f (n))). Chính xác,
f(x) = Θ(g(x)) iff f(x) = O(g(x)) and g(x) = O(f(x))
Ngoài ra còn có các ký hiệu little-oh và little-omega (ω) đại diện cho giới hạn trên và dưới lỏng lẻo của một chức năng.
Để tóm tắt:
f(x) = O(g(x)) (big-oh) có nghĩa là tốc độ tăng trưởng của f(x) là không có triệu chứng ít hơn hoặc bằng đến tốc độ tăng trưởng của g(x).
f(x) = Ω(g(x)) (big-omega) có nghĩa là tốc độ tăng trưởng của f(x) là không có triệu chứng lớn hơn hoặc bằng tốc độ tăng trưởng của g(x)
f(x) = o(g(x)) (little-oh) có nghĩa là tốc độ tăng trưởng của f(x) là không có triệu chứng ít hơn tốc độ tăng trưởng của g(x).
f(x) = ω(g(x)) (ít omega) có nghĩa là tốc độ tăng trưởng của f(x) là không có triệu chứng lớn hơn tốc độ tăng trưởng của g(x)
f(x) = Θ(g(x)) (theta) có nghĩa là tốc độ tăng trưởng của f(x) là không có triệu chứng tương đương với tốc độ tăng trưởng của g(x)
Để thảo luận chi tiết hơn, bạn có thể đọc định nghĩa trên Wikipedia hoặc tham khảo sách giáo khoa cổ điển như Giới thiệu về thuật toán của Cormen et al.
Có một cách đơn giản (một mẹo, tôi đoán vậy) để nhớ ký hiệu nào có nghĩa là gì.
Tất cả các ký hiệu Big-O có thể được coi là có một thanh.
Khi nhìn vào một, thanh nằm ở dưới cùng, do đó, nó là một giới hạn dưới (tiệm cận).
Khi nhìn vào một, thanh rõ ràng là ở giữa. Vì vậy, nó là một (không triệu chứng) ràng buộc chặt chẽ.
Khi viết tay O, bạn thường hoàn thành ở trên cùng và vẽ một hình vuông. Do đó O(n) là giới hạn trên của hàm. Công bằng mà nói, cái này không hoạt động với hầu hết các phông chữ, nhưng nó là sự biện minh ban đầu của các tên.
Xem thêm: Văn Hóa Công Ty Là Gì, Văn Hóa Doanh Nghiệp Là Gì
Thay vì cung cấp một định nghĩa lý thuyết, đã được tóm tắt rất hay ở đây, tôi sẽ đưa ra một ví dụ đơn giản:
Giả sử thời gian chạy của f(i) là O(1). Dưới đây là một đoạn mã có thời gian chạy tiệm cận là Θ(n). Nó luôn luôn gọi hàm f(…)n lần. Cả giới hạn dưới và giới hạn trên là n.
for(int i=0; iĐoạn mã thứ hai bên dưới có thời gian chạy tiệm cận là O(n). Nó gọi hàm f(…)nhiều nhấtn lần. Giới hạn trên là n, nhưng giới hạn dưới có thể là Ω(1) hoặc Ω(log(n)), tùy thuộc vào những gì xảy ra bên trong f2(i).
for(int i=0; i
A biểu đồ có thể làm cho các câu trả lời trước dễ hiểu hơn:
-Ký hiệu – Cùng thứ tự | Ký hiệu O – Giới hạn trên
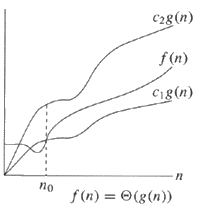
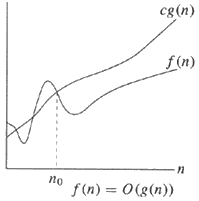
Bằng tiếng Anh,
Ở bên trái, lưu ý rằng có một giới hạn trên và giới hạn dưới là cả hai cùng một thứ tự cường độ (tức là g (n) ). Bỏ qua các hằng số và nếu giới hạn trên và giới hạn dưới có cùng độ lớn, người ta có thể nói một cách hợp lệ f (n) = Θ (g (n)) hoặc f (n) nằm trong theta lớn của g (n) .
Bắt đầu với bên phải, ví dụ đơn giản hơn, nó nói rằng giới hạn trên g (n) chỉ đơn giản là thứ tự cường độ và bỏ qua hằng số c (giống như tất cả ký hiệu O lớn ).
Theta là một cách viết tắt để đề cập đến một tình huống đặc biệt trong đó chữ O và Omega lớn giống nhau.
Do đó, nếu một người yêu cầu The Theta is expression q, thì họ cũng nhất thiết phải tuyên bố rằng Big O is expression q và Omega is expression q.
Tương tự thô:
Nếu: Theta tuyên bố, “Con vật đó có 5 chân.” sau đó nó nói rằng: Big O là đúng (“Con vật đó có ít hơn hoặc bằng 5 chân.”) và Omega là đúng (“Con vật đó có nhiều hơn hoặc bằng 5 chân.”)
Đây chỉ là một sự tương tự thô vì các biểu thức không nhất thiết phải là các số cụ thể, mà thay vào đó là các hàm có độ lớn khác nhau như log (n), n, n ^ 2, (v.v.).
Kết luận: chúng tôi coi O lớn, lớn và lớn Ω là điều tương tự.
Tại sao? Tôi sẽ nói lý do dưới đây:
Đầu tiên, tôi sẽ làm rõ một tuyên bố sai, một số người nghĩ rằng chúng tôi chỉ quan tâm đến sự phức tạp thời gian tồi tệ nhất, vì vậy chúng tôi luôn sử dụng chữ O lớn thay vì lớn. Tôi sẽ nói người đàn ông này là nhảm nhí. Giới hạn trên và dưới được sử dụng để mô tả một chức năng, không được sử dụng để mô tả độ phức tạp thời gian. Hàm thời gian tồi tệ nhất có giới hạn trên và dưới của nó; chức năng thời gian tốt nhất cũng có giới hạn trên và dưới của nó.
Để giải thích rõ ràng mối quan hệ giữa O lớn và lớn, tôi sẽ giải thích mối quan hệ giữa O lớn và o nhỏ trước. Từ định nghĩa, chúng ta có thể dễ dàng biết rằng o nhỏ là tập con của O lớn. Ví dụ:
T (n n ^ 2 + n, chúng ta có thể nói T (n) = O (n ^ 2), T (n) = O (n ^ 3), T (n) = O (n ^ 4). Nhưng đối với o nhỏ, T (n) = o (n ^ 2) không đáp ứng định nghĩa của o nhỏ. Vì vậy, chỉ T (n) = o (n ^ 3), T (n) = o ( n ^ 4) đúng với o nhỏ. T (n) = O (n ^ 2) dự phòng là gì? Nó lớn θ!) ==
Nói chung, chúng ta nói O lớn là O (n ^ 2), khó có thể nói T (n) = O (n ^ 3), T (n) = O (n ^ 4). Tại sao? Bởi vì chúng tôi coi O lớn là lớn θ trong tiềm thức.
Tương tự, chúng tôi cũng coi lớn Ω là lớn θ trong tiềm thức.
Trong một từ, chữ O lớn, lớn θ và lớn Ω không giống nhau từ các định nghĩa, nhưng chúng là cùng một thứ trong miệng và não của chúng ta.
Xem thêm: Freesync Là Gì – Amd Freesync Và Những Điều Bạn Cần Biết
Sử dụng giới hạn
Chúng ta hãy xem xét f(n) > 0 và g(n) > 0 cho tất cả n. Bạn có thể cân nhắc điều này vì thuật toán thực nhanh nhất có ít nhất một thao tác và hoàn thành việc thực hiện sau khi bắt đầu. Điều này sẽ đơn giản hóa phép tính, bởi vì chúng ta có thể sử dụng giá trị (f(n)) thay vì giá trị tuyệt đối (|f(n)|).
f(n) = O(g(n))
Chung :
f(n) 0 ≤ lim ──────── Dành cho g(n) = n :
f(n) 0 ≤ lim ──────── Ví dụ :
Expression Value of the limit————————————————n = O(n) 11/2*n = O(n) 1/22*n = O(n) 2n+log(n) = O(n) 1n = O(n*log(n)) 0n = O(n²) 0n = O(nⁿ) 0Counterexamples :
Expression Value of the limit————————————————-n ≠ O(log(n)) ∞1/2*n ≠ O(sqrt(n)) ∞2*n ≠ O(1) ∞n+log(n) ≠ O(log(n)) ∞
f(n) = Θ(g(n))
Chung :
f(n) 0 Dành cho g(n) = n :
f(n) 0 Ví dụ :
Expression Value of the limit————————————————n = Θ(n) 11/2*n = Θ(n) 1/22*n = Θ(n) 2n+log(n) = Θ(n) 1Counterexamples :
Expression Value of the limit————————————————-n ≠ Θ(log(n)) ∞1/2*n ≠ Θ(sqrt(n)) ∞2*n ≠ Θ(1) ∞n+log(n) ≠ Θ(log(n)) ∞n ≠ Θ(n*log(n)) 0n ≠ Θ(n²) 0n ≠ Θ(nⁿ) 0
Chuyên mục: Hỏi Đáp