Nơi tổng hợp và chia sẻ những kiến thức liên quan tới giải thuật nói chung và lý thuyết khoa học máy tính nói riêng.
Bạn đang xem: Bfs là gì
Đồ thị — Introduction to Algorithmic Graph Theory
September 26, 2015 in Uncategorized | No comments
Trong bài này và loạt bài tiếp theo chúng ta sẽ làm quen với đồ thị và các thuật toán với đồ thị. Đồ thị là một đối tượng tổ hợp (combinatorial object) được nghiên cứu và ứng dụng rất nhiều trong thực tế (có lẽ hơi thừa khi viết điều này). Phần này chúng ta sẽ:
Làm quen với các khái niệm cơ bản gắn với đồ thị Cách biểu diễn đồ thị trong máy tính để chúng ta có thể thao tác với nóDuyệt đồ thị theo chiều rộng (Breadth First Search)Duyệt đồ thị theo chiều sâu (Depth First Search)
Bạn đọc có thể bỏ qua các phần mà các bạn đã quen thuộc. Note của Jeff Erickson vẫn là tài liệu tham khảo chính của bài này.
Các khái niệm
Một đồ thị, kí hiệu là $G(V,E)$, gồm hai thành phần:
Tập hợp $V$, bao gồm các đối tượng, được gọi là tập hợp các đỉnh (vertex) của đồ thịTập hợp $E subseteq V^2$, bao gồm một cặp các đỉnh, được gọi là tập hợp các cạnh (vertex) của đồ thị
Ta sẽ kí hiệu $n,m$ lần lượt là số đỉnh và số cạnh của đồ thị, i.e, $|V| = n, |E|= m$. Số đỉnh của đồ thị đôi khi ta cũng gọi là bậc của đồ thị (order of the graph).
Các đỉnh ta sẽ kí hiệu bằng các chữ in thường như $u,v,x,y,z$. Cạnh giữa hai đỉnh $u,v$ có thể là vô hướng hoặc có hướng. Trong trường hợp đầu ta sẽ kí hiệu cạnh là $uv$, còn trong trường hợp sau ta sẽ kí hiệu là $u ightarrow v$ để chỉ rõ hướng của cạnh là từ $u$ đến $v$. Thông thường khi ta nói cạnh thì ta ám chỉ cạnh vô hướng còn với một cạnh có hướng ta sẽ gọi nó là một cung (arc). Hình $(1,2)$ của hình dưới đây biểu diễn một đồ thị vô hướng (các cạnh là vô hướng) và hình $(3)$ phải của hình dưới đây biểu diễn một đồ thị có hướng.
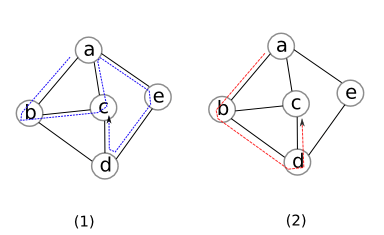
Một đồ thị vô hướng được gọi là liên thông (connected) nếu tồn tại một đường đi giữa mọi cặp điểm. Một đồ thị có hướng gọi là liên thông (yếu) nếu đồ thị vô hướng thu được từ đồ thị đó bằng cách bỏ qua hướng của cạnh là liên thông. Một đồ thị có hướng gọi là liên thông mạnh (strongly connected) nếu tồn tại một đường đi có hướng giữa mọi cặp điểm. Hiển nhiên nếu một đồ thị có hướng liên thông mạnh thì nó cũng liên thông yếu. Tuy nhiên điều ngược lại chưa chắc đúng (ví dụ?). Ví dụ đồ thị $(1)$ dưới đây là không liên thông, đồ thị $(2)$ liên thông, đồ thị $(3)$ liên thông yếu (nhưng không mạnh) và đồ thị $(4)$ liên thông mạnh.
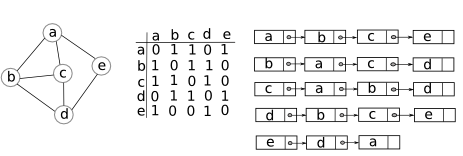
Ta còn có thể kết hợp cách biểu diễn danh sách kề với một vài cấu trúc dữ liệu khác. Cụ thể, thay vì dùng danh sách liên kết để biểu diễn các đỉnh kề với một đỉnh $u$, ta còn có thể dùng bảng băm hoặc cấu trúc cây để biểu diễn. Trong khuôn khổ các bài viết ở đây, ta ít dùng (hoặc không dùng) các cấu trúc như vậy.
Ngoài ra ta có thể biểu diễn đồ thị bằng cách liệt kê tất cả các cặp $(u,v)$ thỏa mãn $uv in E$. Cách biểu diễn này có bộ nhớ là $O(m)$. Tuy nhiên, việc thực hiện các thao tác cơ bản trong cách biểu diễn này sẽ rất tốn kém. Đôi khi, ta có thể kết hợp cách biểu diễn này với cách biểu diễn danh sách kề để tận dụng ưu thế của cả hai cách biểu diễn mà bộ nhớ vẫn là tuyến tính.
Duyệt đồ thị
Problem 1: Cho một đồ thị $G(V,E)$ và một đỉnh $s in V$, in ra các đỉnh $v$ thỏa mãn tồn tại một đường đi từ $s$ tới $v$.
Ta gọi bài toán trên là bài toán duyệt đồ thị từ một đỉnh $s$. Để đơn giản, ta sẽ giả sử đồ thị là liên thông. Trường hợp đồ thị không liên thông sẽ được mở rộng ở cuối phần này. Cách thức chung để duyệt đồ thị như sau: Ta sẽ sử dụng 2 loại nhãn để gán cho các đỉnh của đồ thị: chưa thăm (unvisited) và đã thăm (visited). Ban đầu tất cả các đỉnh được đánh dấu là chưa thăm (unvisited). Ta sẽ duy trì một tập hợp $C$ (thực thi tập $C$ thế nào ta sẽ tìm hiểu sau), ban đầu khởi tạo rỗng. Ta sẽ thực hiện lặp 2 bước sau:
Lấy ra một đỉnh $u$ trong $C$ (thủ tục Remove$(C)$ dưới đây). Đánh dấu $u$ là đã thăm (visited). Đưa các hàng xóm của $u$ có nhãn chưa thăm vào trong $C$. Thủ tục Add$(C,v)$ dưới đây sẽ đưa đỉnh $v$ vào trong tập $C$.
Thuật toán dừng khi $C = emptyset$. Giả mã như sau:
GenericGraphTraverse($G(V,E),s$): mark all vertices unvisited Add$(C,s)$ while $C ot= emptyset$ $u leftarrow$ Remove$(C)$ $ll(*)gg$ if $u$ is unvisited mark $u$ visited for all $uv in E$ and $v$ is unvisited $ll(**)gg$ Add$(C,v)$
Remark: Một đỉnh có thể được đưa nhiều lần vào tập $C$ (do đó $C$ không hẳn là tập hợp vì có nhiều phần tử giống nhau). Ví dụ xét 3 đỉnh $u,v,w$ đôi một kề nhau. Đỉnh $u$ được lấy ra từ $C$ đầu tiên; đánh dấu $u$ là đã thăm. Ngay sau đó, $v$ và $w$ sẽ được đưa vào $C$. Tiếp theo, lấy $v$ ra khỏi $C$ và đánh dấu $v$ là đã thăm. Lúc này ta lại tiếp tục đưa $w$ vào $C$ một lần nữa vì theo giả mã trên, $w$ là hàng xóm của $v$ và có nhãn chưa thăm. Ở đây, ta sẽ không kiểm tra xem một đỉnh đã nằm trong $C$ hay chưa trước khi đưa vào $C$.
Xem thêm: Acorn Là Gì – Acorn Trong Tiếng Tiếng Việt
Từ giả mã trên, ta thấy, tập $C$ lưu các đỉnh kề với ít nhất một đỉnh đã thăm.
Phân tích thuật toán: Giả sử rằng ta sử dụng một cấu trúc để thực thi $C$ sao cho việc thêm vào hoặc lấy một đỉnh bất kì (dòng $(*)$ và dòng cuối cùng) được thực hiện trong thời gian $O(1)$ (ví dụ nếu thưc thi $C$ bằng danh sách liên kết thì thêm vào hoặc lấy ra đỉnh ở đầu danh sách có thể được thực hiện trong thời gian $O(1)$). Ta có một vài nhận xét sau:
Các đỉnh đã được lấy ra khỏi $C$ và bị đánh dấu là đã thăm thì nó sẽ không bao giờ được đưa trở lại tập $C$ nữa.Mỗi lần đỉnh $v$ được đưa vào $C$, một hàng xóm của nó sẽ bị đánh dấu là đã thăm. Do đó, đỉnh $v$ sẽ bị đưa vào $C$ không quá $d(v)$ lần.Mỗi khi lấy một đỉnh $u$ ra khỏi $C$, ta sẽ duyệt qua tất cả các hàng xóm của $u$. Thao tác này mất thời gian $O(d(u))$. Theo nhận xét 1, phép duyệt này chỉ được thực hiện tối đa 1 lần.
Từ các nhận xét trên, ta suy ra tổng thời gian tính toán của thuật toán là $O(sum_{u in V}d(u)) = O(m)$.
Trong trường hợp đồ thị không liên thông, ta phải duyệt qua từng thành phần liên thông một. Do đồ thị có tối đa $n$ thành phần liên thông, ta có:
Nếu ta thực thi $C$ bằng danh sách liên kết thì có lẽ không có gì thú vị cả. Tuy nhiên, nếu ta thực thi $C$ bằng hàng đợi (Queue) hoặc ngăn xếp (Stack) thì ta sẽ thu được một số tính chất thú vị từ đồ thị. Trường hợp ta thực thi $C$ bằng hàng đợi, ta gọi thuật toán là duyệt theo chiều rộng (Breath First Search – BFS). Trường hợp ta thực thi $C$ bằng ngăn xếp, ta gọi thuật toán là duyệt theo chiều sâu (Depth First Search – DFS). Sau đây ta sẽ thảo luận cả hai thuật toán.
Thuật toán duyệt theo chiều rộng BFS
Như đã nói ở trên, thuật toán BFS sẽ thực thi $C$ bằng hàng đợi. Ta sẽ thay thủ tục Add$(C,v)$ bằng thủ tục Enqueue$(C,v)$ và thủ tục Remove$(C)$ bằng thủ tục Dequeue$(C)$. Ngoài khung cơ bản như thuật toán ở trên, ta sẽ gán cho mỗi đỉnh $v$ một nhãn $d$. Giá trị của $d$, như ta sẽ chỉ ra dưới đây, là khoảng cách ngắn nhất từ $s$ tới $v$. Giả mã như sau:
BFS($G(V,E),s$): for each $v in V$ $d leftarrow +infty$ $Cleftarrow$ an empty Queue Enqueue$(C,s)$ $d leftarrow 0$ while $C ot= emptyset$ $u leftarrow$ Dequeue$(C)$ if $u$ is unvisited mark $u$ visited for all $uv in E$ and $v$ is unvisited $ll(**)gg$ Enqueue$(C,v)$ $d leftarrow d+1$
Code của giả mã bằng C:
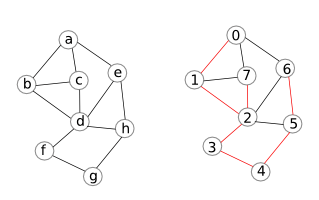
#define UNVISITED 0#define VISITED 1#define TRUE 1#define FALSE 0#define INFTY 1000000// the vertex list data structure, it is a linked listtypedef struct vlist{int v;// vertex v is adjacent to the index of the liststruct vlist *next;}vlist;vlist **G;int n;// the number of veritcesint m;// the number of edgesint *D; // the distance of vertices from BFSint* mark; // an array to mark visited verticestypedef struct Queue{int *storage;int back, front;}Queue;void bfs(int s){printf(“executing bfs….. “);D = (int *)(malloc(n*sizeof(int)));int i = 0;for(; i v;if(mark == UNVISITED){D = D+1;enqueue(Q,v);}runner = runner->next;}}}printf(“done bfs “);}////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////THE QUEUE INTERFACES////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////Queue *init_queue(int size){Queue *Q = malloc(sizeof(Queue));Q->storage = (int *)malloc(size*sizeof(int));Q->front = 0;Q->back = -1;return Q;}void enqueue(Queue *Q, int elem){Q->back ++;Q->storageback> = elem;}int dequeue(Queue *Q){if(is_queue_empty(Q)) {printf(“nothing to dequeue “);exit(0);}int elem = Q->storagefront>;Q->front++;return elem;}int is_queue_empty(Queue* Q){return Q->back front? TRUE : FALSE;}Ví dụ ta thực thi thuật toán trên với đồ thị trong hình bên trái và kết qủa thu được trong hình bên phải. Các số ứng với các đỉnh tương ứng là nhãn của các đỉnh đó. Những cạnh màu đỏ laf những cạnh mà $v$ có nhãn unvisited ở dòng $(**)$ được thăm bởi BFS.
Ngoài thủ tục lặp DFS sử dụng ngăn xếp như trên, có lẽ một trong số chúng ta cũng khá quen thuộc với thủ tục thực thi DFS sử dụng đệ quy sau:
Code của giả mã bằng
void recursive_dfs(int s){printf(“visiting %d “,s);mark = VISITED;// loop through neighbors of sint v = 0;for(; v Ta thấy cách thứ hai đơn giản hơn do không phải thực thi Stack. Tuy nhiên, cách này sẽ sử dụng nhiều Call Stack của máy tính và trong trường hợp độ sâu đệ quy lớn có thể gây ra Stack Overflow.
Phát hiện các thành phần liên thông
Một trong những ứng dụng đơn giản nhất để duyệt đồ thị là phát hiện ra các thành phần liên thông. Để phát hiện ra các thành phần liên thông của đồ thị (vô hướng), ta thực hiện lặp lại thao tác sau: chọn một đỉnh chưa thăm $u$ và thực hiện thăm các đỉnh trong thành phần liên thông chứa $u$. Thủ tục sau đây trả lại số thành phần liên thông của đồ thị đầu vào $G(V,E)$.
ConnecteComponents($G(V,E)$): mark all vertices unvisited $count leftarrow 0$ for all vertices $sin V$ if $s$ is unvisited GraphTraversal($G(V,E),s$) $countleftarrow count+1$ return $count$
Code C:
int connected_component(){memset(mark, UNVISITED, (n+1)*sizeof(int)); // mark all vertices unvisitedint s = 0;int count = 0;for(; s Code đầy đủ: list-representation, matrix-representation.
Xem thêm: Hướng đối Tượng Là Gì, Lập Trình Hướng đối Tượng
Tham khảo
Jeff Erickson, Graph Lecture Note, UIUC. Diestel, Reinhard. Graph theory. 2005. Grad. Texts in Math (2005). Cormen, Thomas H.; Leiserson, Charles E., Rivest, Ronald L., Stein, Clifford. Introduction to Algorithms (2nd ed.), Chapter 23. MIT Press and McGraw-Hill (2001). ISBN 0-262-03293-7.
Chuyên mục: Hỏi Đáp