Trọng tâm tam giác là gì Update 11/2024

Một trong những dạng bài toán phổ biến nhất và cũng không kém phần thách thức với các học sinh ở phần hình học phổ thông thường là các bài toán liên quan đến trọng tâm. Với dạng hình thường gặp nhất là trọng tâm hình tam giác. 

Chính vì lý do này, hôm nay thienmaonline.vn xin gửi đến bạn một bài viết tổng quát nhất về định nghĩa trọng tâm là gì, trọng tâm hình tam giác, cũng như cách tính trọng tâm, các công thức liên quan đến trọng tâm hình tam giác.

Bạn đang xem: Trọng tâm tam giác là gì

1.TRỌNG TÂM LÀ GÌ?

Theo sách giáo khoa hiện hành, từ năm học lớp 7 học sinh đã được tiếp xúc với trọng tâm. Định nghĩa trọng tâm được sách giáo khoa ghi lại như sau: “Trong 1 tam giác có 3 đường trung tuyến. 3 đường trung tuyến này cùng đi qua một điểm, điểm này được gọi là trọng tâm của tam giác”.

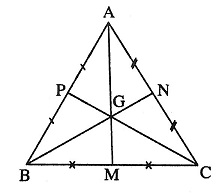
Lấy ví dụ tam giác ABC với 3 đường trung tuyến lần lượt là AM, BN, CP. 3 đường trung tuyến của tam giác ABC này lần lượt đi qua giao điểm G. G chính là trọng tâm của tam giác ABC.

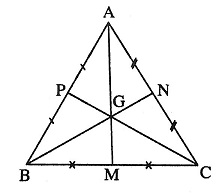
2. CÁCH XÁC ĐỊNH TRỌNG TÂM TAM GIÁC

Trọng tâm hình tam giác có một tính chất quan trọng cần nhớ như sau: “Khoảng cách từ trọng tâm tam giác đến 3 đỉnh của hình tam giác bằng ⅔ độ dài đường trung tuyến tương ứng với đỉnh đó”.

Xem thêm: Khu Ẩm Thực Royal City – KháM Phá Khu Phố ẨM ThựC TạI Royal City

Từ tính chất này, ta có 2 cách để xác định trọng tâm của một tam giác. Lấy ví dụ tam giác ABC với 3 đường trung tuyến AM, BN, CP và G là trọng tâm tam giác ABC. 

Cách 1: 

Xác định trung điểm M của cạnh BC sao cho M chia BC thành 2 đoạn bằng nhau MC = MBNối đỉnh A với trung điểm M, ta có đường trung tuyến AMThực hiện xác định trung điểm và nối đỉnh tương tự với các trung tuyến khácGiao điểm của 3 đường trung tuyến được gọi là điểm G. Từ đây chứng minh được G là trọng tâm ABC. 

Cách 2:

Xác định trung điểm M của cạnh BC sao cho M chia BC thành 2 đoạn bằng nhau MC = MBNối đỉnh A với trung điểm M, ta có đường trung tuyến AMTrên trung tuyến AM, chọn điểm G sao cho AG = ⅔ AMDựa trên tính chất trọng tâm tam giác, ta suy ra G chính là trọng tâm tam giác ABC. 

3.TRỌNG TÂM TRONG CÁC HÌNH ĐẶC BIỆT

Trọng tâm vốn là một điểm rất đặc biệt và trọng tâm trong các hình tam giác đặc biệt như tam giác vuông, cân hay tam giác đều còn khiến đường trung tuyến ứng với trọng tâm có đến vài vai trò khác nhau trong một hình. 

Dưới đây là một số ví dụ về trọng tâm trong các hình học đặc biệt mà rất có thể bạn sẽ gặp trong chương trình học phổ thông của mình:

Trọng tâm trong tam giác vuông

Ta có tam giác ABC, vuông tại B. Từ điểm B ta vẽ đường trung tuyến BA, sao cho A chia CD thành hai đoạn AD = AC. Do BA là đường trung tuyến của góc vuông nên ta có BA = ½ CD, tức BA = AD = AC. Từ đó ta có hai tam giác ABD và tam giác ABC cân tại A. 

Trọng tâm trong tam giác cân

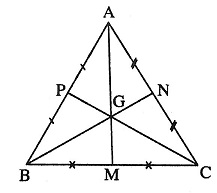
Tiếp tục lấy ví dụ tam giác ABC cân tại A. Gọi G là trọng tâm tam giác cân ABC. Do ABC cân tại A nên AG lúc này vừa đóng vai trò là đường trung tuyến, đường cao và cả đường phân giác của tam giác ABC. Ta có hệ quả từ trọng tâm này như sau: 

Góc BAG = Góc CAGTrung tuyến AG vuông góc với cạnh BC

Trọng tâm trong tam giác đều

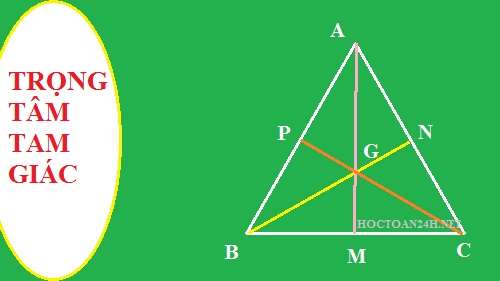
Giả sử tam giác đều ABC có G là giao điểm ba đường trung tuyến. Do tính chất đặc biệt của tam giác đều (3 cạnh bằng nhau) nên điểm G có tới 4 vai trò: là trọng tâm, trực tâm, tâm đường tròn ngoại và nội tiếp của tam giác ABC.

Trọng tâm trong hình tứ diện

Tại các bậc học cao hơn, học sinh sẽ được tiếp xúc với các loại trọng tâm khó hơn. Điển hình như với các bài tập dạng trọng tâm trong hình tứ diện. 

Giả sử ta có hình tứ diện ABCD với G là trọng tâm. Trọng tâm trong hình tứ diện này là giao điểm của 4 đường thẳng nối đỉnh và trọng tâm của các tam giác đối diện với nhau. 

4. BÀI TẬP LUYỆN TẬP

Để hiểu rõ hơn về trọng tâm, bạn có thể tham khảo bài tập sau đây: Tam giác ABC có trung tuyến BM = CN. Hai trung tuyến trên cắt nhau tại G. Bạn hãy chứng minh tam giác ABC cân tại A.

Xem thêm: Thẻ Div Trong Html Là Gì – Cách Dùng Thẻ Div Trong Html Từ A Đến Z

Bài giải: 

Do BM và CN là trung tuyến tam giác ABC, giao nhau tại G nên BG / BM = CG/ CN = ⅔Do BM = CN => BG=CN và GN=GMTrong tam giác BNG và tam giác CGM: BG=CN, GN=GM và góc BGN bằng góc CGM (góc đối đỉnh)Như vậy, tam giác BNG và tam giác CGM đồng dạng => BN = CM => AB = AC. Như vậy ABC là tam giác cân tại A.

Như vậy, với các kiến thức cơ bản và bài tập luyện tập làm quen nói trên, thienmaonline.vn hi vọng bạn đọc đã có cho mình sự hiểu biết nhất định về trọng tâm. Nắm vững những kiến thức kể trên có thể giúp ích rất nhiều trong việc giải các bài tập hình học từ cơ bản đến nâng cao. Rất mong bạn đọc sẽ vận dụng hợp lý chúng để đạt được kết quả cao nhất trong các kì thi của mình!

Chuyên mục: Hỏi Đáp